Pearson Correlation Calculator
Pearson Correlation Calculator helps you to solve pearson correlation coefficient between two variables. So, provide the input values in the below box and press on the calculate button available next to the input to get the result in a short span of time.
Pearson Correlation Calculator
Pearson Correlation Calculator: Pearson Correlation Coefficient is a concept in statistics that is used to measure the strength of linear association between two variables. Do you think finding pearson correlation coefficient is tough and complicated? Not anymore, because we have come up with the Pearson Correlation Calculator that saves your valuable time and gives output with lengthy explanation fastly. Here, you will find the handy calculator tool which is helpful to calculate the pearson correlation. We have also included some solved examples for the better understanding of students.
How to Calculate Pearson Correlation Coefficient?
Pearson Correlation Coefficients are used in statistics to measure how strong the relationship between two sets of data. It is represented by r. The following are the easy and simple steps used to solve the pearson correlation coefficient value. Have a look at them and follow while solving the pearson correlation
- Take two sets of data i.e x and y.
- Find the mean of x and y.
- Mean of data item = Sum of all data values/ number of data items.
- Using this formula, compute xmean, ymean.
- The formula to get the r value is
- r = Σi [(xi - xmean)(yi - ymean] / √Σi(xi - xmean)2 √Σi(yi - ymean)2
- Substitute the values and perform math operations to get the r value.
Pearson Correlation Coefficient Formula
Pearson Correlation Coefficient is used to check the linear dependency between the data set. It is also called as Product Pearson Moment Correlation Coefficient. If value of Pearson Correlation Coefficient is +1, then data is positively correlated. If it is -1, then data has negatively correlated. If the pearson correlation is zero, then data is said to be not related.
The formula to check the pearson correlation for sample data is

where, xmean is the mean of x data set.
ymean is the mean of y data set.
Example
Question: Find the value of correlation coefficient? Marks obtained by 6 students in algebra and trigonometry are Algebra (x) = {15, 16, 12, 10, 8, 6}, Trigonometry (y) = {18, 11, 10, 20, 17, 19}
Solution:
Giveb values are
Algebra (x) = {15, 16, 12, 10, 8, 6}, Trigonometry (y) = {18, 11, 10, 20, 17, 19}
Pearson Correlation Coefficient formula is
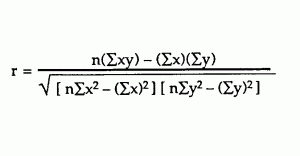
Where,
r = Pearson correlation coefficient
x = Values in the first set of data
y = Values in the second set of data
n = Total number of values.
| x | y | x2 | y2 | xy |
|---|---|---|---|---|
| 15 | 18 | 225 | 324 | 270 |
| 16 | 11 | 256 | 121 | 176 |
| 12 | 10 | 144 | 100 | 120 |
| 10 | 20 | 114 | 400 | 200 |
| 8 | 17 | 64 | 289 | 126 |
| 6 | 19 | 36 | 361 | 114 |
| ∑x = 67 | ∑y = 95 | ∑x2 = 825 | ∑y2 = 1595 | ∑xy = 1016 |
substituting the values in the formula
= 6(1016) - (67)(95) / √[6 * 825 - (67)2] [6 * 1595 - (95)2
= 6096 - 6365 / √(4950 - 4489)(9570 - 9025
= -269 / √(461)(545
= -269/ 501.2
= -0.5367
People of any mathematical knowledge can solve the concepts easily taking the help of our calculators at Onlinecalculator.guru

FAQs on Pearson Correlation Calculator
1. Why would you use a Pearson correlation?
Pearson Correlation is used when you have two quantitative variables and you wish to see if there is a linear relationship between those variables.
2. What are the 4 types of correlation?
We have 4 types of correlations. They are Pearson Correlation, Kendall rank correlation, Spearman correlation, and Point Biserial correlation.
3. What is considered a weak correlation?
A weak correlation means that as one variable increases or decreases, there is a lower likelihood of there being relationship with the second variable.
4. What is pearson correlation coefficient formula?
Pearson correlation coefficient is reffered as r. It is a statistical formula that measures the strength between relationships and variables. Pearson Correlation Coefficient formula is
r = [n(∑xy) - (∑x)(∑y)] / √(n∑x2 - (∑x)2) (n∑y2 - (∑y)2).