Polynomial Root Calculator
The Polynomial Roots Calculator will display the roots of any polynomial with just one click after providing the input polynomial in the below input box and clicking on the calculate button.
Ex:
Here are some samples of Polynomial Root calculations.
- Polynomial Root of 10b^4+3b^2-11
- Polynomial Root of 10x^2+4x+12
- Polynomial Root of 10x^2-2x-3
- Polynomial Root of 10x^2-5x+10
- Polynomial Root of 10x^2-9x-6
- Polynomial Root of 10x^2-x+9
- Polynomial Root of 11x^2+3x+1
- Polynomial Root of 11x^2+5x+1
- Polynomial Root of 11x^2-12x-10
- Polynomial Root of 11x^2-4x-1
- Polynomial Root of -12.31x^2+1.32x+31.02
- Polynomial Root of 128+112t-16t^2
- Polynomial Root of 12x^2-120x+209
- Polynomial Root of 12x^2-132x+252
- Polynomial Root of 12x^2-144x+299
- Polynomial Root of 12x^2-156x+480
- Polynomial Root of 12x^2-168x+405
- Polynomial Root of 12x^2-192x+527
- Polynomial Root of 12x^2-228x+740
- Polynomial Root of 12x^2-240x+819
- Polynomial Root of 12x^2-264x+989
- Polynomial Root of 12x^2-4x-10
- Polynomial Root of 12x^2-72x+77
- Polynomial Root of 12x^2-9x+4
- Polynomial Root of -13x^2-130x-273
- Polynomial Root of 14x^2+42x+70
- Polynomial Root of 154-10t-16t^2
- Polynomial Root of -16t^2+105t-34
- Polynomial Root of -16t^2+12t+40
- Polynomial Root of -16t^2+12t+900
- Polynomial Root of -16t^2+144
- Polynomial Root of -16t^2+151t-88
- Polynomial Root of -16t^2+15t+12
- Polynomial Root of -16t^2+16t+480
- Polynomial Root of -16t^2+17t-4
- Polynomial Root of -16t^2+195t-87
- Polynomial Root of -16t^2+200t+50
- Polynomial Root of -16t^2+20t+24
- Polynomial Root of -16t^2+20t+6
- Polynomial Root of -16t^2+215t-97
Polynomial Root Calculator: Finding roots of polynomials was never that easy! but not anymore because now we have an online calculator to solve all complex polynomial root calculations for free of charge. This online & handy Polynomial Root Calculator factors an input polynomial into various square-free polynomials then determines each polynomial either analytically or numerically. Also, the tool will show you the work and detailed explanation. So, try our free tool & find out the roots of a polynomial easily at a faster pace.
What is meant by Polynomial Root?
In mathematics, Usually, the roots are defined as the roots/variable value of the quadratic equation. We all know that the equation with a higher degree of two is known as the quadratic equation where it should be in the form ax^2 + bx+ c = 0.
Here a, b, and c are the coefficients of the equation and the value of 'a' should not be equal to 0, and x is the variable. The solution derived for the value of x is described as the roots of the quadratic equation. The root values can be normally taken using the formula,
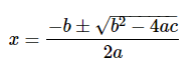
How to calculate a polynomial root?
A root of a polynomial is a value for which the polynomial is Zero '0'. A polynomial of degree n can have between 0 and n roots. The roots of a polynomial are also called its zeroes because F(x)=0.
The general principle of root calculation is to determine the solutions of the equation polynomial = 0 as per the studied variable (where the curve crosses the y=0 axis). The calculation of polynomial roots generally involves the calculation of its discriminant.
The root values can be normally taken using the quadratic equation formula,
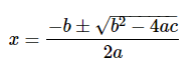
substitute the respective coefficient values in the formula and find out the roots for the given quadratic equation easily & effortlessly.
Also, You can use our site ie., onlinecalculator.guru provided a trusted and reliable best calculator ie., Polynomial Root Calculator for all your complex calculations & make them easy & simple when your homework or assignments.

FAQs on Polynomial Root Calculator
1. How to determine a discriminant?
Use the formula of the polynomial discriminant & substitute the values in it to get the actual result easily in less time. The formula to calculate the Polynomial discriminant for the quadratic equation is Δ = b^2−4ac.
2. What is zero for a polynomial?
A zero of a polynomial function F is a solution x such that F(x)=0, so it is also known as root.
3. What is the nth degree polynomial?
The order of a polynomial (2nd order 2 or quadratic, 3rd order or cubic, 4th order, etc.) is the value of its largest exponent.
4. Where do I find a detailed solution to check for prime polynomials?
You can find a detailed solution to check if the polynomial is Prime or not on our page.