Capacitance Formulas

1. Capacitance of a conductor

Capacity of storing charge
C = \(\frac{Q}{V}\)
Unit → farad = \(\frac{\text { coulomb }}{\text { volt }}\)

2. Capacitance of a spherical conductor

C = 4πε₀R
R → Radius of conductor.

3. Common potential when two charged conductors are connected

C = C₁ + C₂
Q = Q₁ + Q₂ = C₁V₁ + C₂ V₂
Common potential
V = \(\frac{\mathrm{C}_{1} \mathrm{V}_{1}+\mathrm{C}_{2} \mathrm{V}_{2}}{\mathrm{C}_{1}+\mathrm{C}_{2}}\)
Charge transferred
ΔQ = \(\frac{C_{1} C_{2}}{C_{1}+C_{2}}\) (V₁ – V₂)
Energy loss
ΔU = \(\frac{1}{2} \frac{C_{1} C_{2}}{C_{1}+C_{2}}\) (V₁ – V₂)²

4. Capacitor (condenser)

An arrangement of conductors for increasing the capacitance. It has two conductors placed nearby, one is charged and the other is earthed.

5. Parallel plate capacitor

C = \(\frac{\epsilon_{0} A}{d}\), C_m = ε_r = \(\left(\frac{\epsilon_{0} A}{d}\right)\) = ε_rC
If a dielectric of thickness t is placed in between, then
C = \(\frac{\epsilon_{0} A}{\left(d-t+\frac{t}{\epsilon_{r}}\right)}\)
(a)

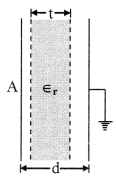
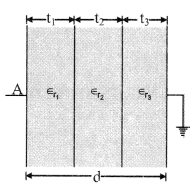
If slabs of thickness t₁, t₂, t₃ …. t_n of dielectric constant’s ε_r1, ε_r2, …… ε_rn are placed in between
C = \(\frac{\epsilon_{0} A}{\left(\frac{t_{1}}{\epsilon_{r_{1}}}+\frac{t_{2}}{\epsilon_{r_{2}}}+\ldots .+\frac{t_{n}}{\epsilon_{r_{n}}}\right)}\)
and d = t₁ + t₂ + t₃ + …. + t_n
(b)

6. Spherical capacitor

When outer spherical shell is earthed
C = 4πε₀ε_r \(\frac{\mathrm{R}_{1} \mathrm{R}_{2}}{\mathrm{R}_{2}-\mathrm{R}_{1}}\) ; R₂ > R₁
When inner sphere is earthed
C = 4πε₀ε_r \(\frac{\mathrm{R}_{1} \mathrm{R}_{2}}{\mathrm{R}_{2}-\mathrm{R}_{1}}\) + 4πε₀R₂

7. Cylinderical condenser

C = \(\frac{2 \pi \epsilon_{0} \epsilon_{\mathrm{r}} \ell}{\log _{\mathrm{c}}\left(\mathrm{R}_{2} / \mathrm{R}_{1}\right)}\)

8. Capacitance of a two wire line

C = \(\frac{\pi \epsilon_{0} \epsilon_{1} \ell}{\log _{e}(d / r)}\) (d >> r)
l → length of each wire
d → distance between wires
r → radius of each wires

9. Multiplate capacitor

C = (n – 1) \(\frac{\epsilon_{0} \in_{r} A}{d}\)
A → area of each plate.

10. Energy stored in a capacitor

U = \(\frac{1}{2}\) CV² = \(\frac{1}{2}\) QV = \(\frac{1}{2} \frac{Q^{2}}{C}\)
This energy resides in electric field. Energy density of electric field
U = \(\frac{1}{2}\) εE² = \(\frac{\text { Total Energy }}{\text { Volume }}\)

11. Combination of capacitor

Series combination
\(\frac{1}{C}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\ldots \ldots+\frac{1}{C_{n}}\)
Q₁ = Q₂ = …….. = Q
V = V₁ + V₂ + V₃+ ……… + V_n
Parallel combination
C = C₁ + C₂ + …….. C_n
V₁ = V₂ = …….. = V
Q = Q₁ + Q₂ + Q₃ + …….. + Q_n

12. Charging and discharging of a capacitor through a resistance

Charging
q = q₀ (1 – e^-t/RC)
V = V₀ (1 – e^-t/RC)

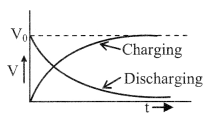
I = I₀ e^-t/RC, I₀ = \(\frac{V_{0}}{R}\)
V → P.d. across capacitor
q → charge on the capacitor
I → current through the capacitor

Discharging
q = q₀ e^-t/RC
V = V₀ e^-t/RC
I = – I₀ e^-t/RC

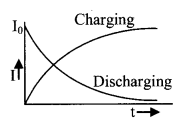
Time constant
while charging
τ = RC, time in which q = 0.63Q, V = 0.63V₀ and I = 0.37I₀
while discharging q = 0.37Q, V = 0.37V₀ and I = 0.37I₀

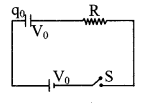
• In charging energy supplied by the battery up to steady state is V₀q₀
• Energy stored in capacitor as a electric field is \(\frac{1}{2}\)V₀q₀
• Energy loss during charges = \(\frac{1}{2}\) V₀q₀

13. Force of attraction between the plates of a capacitor

F = \(\frac{1}{2}\) εE² A = \(\frac{Q^{2}}{2 \in A}=\frac{1}{2} \frac{C V^{2}}{d}\)
F = \(\frac{\sigma^{2}}{2 \epsilon}\)A

Seek help regarding concepts that you never seemed to understand in an efficient manner from Onlinecalculator.guru and clarify all your concerns.