Chemical Energetics Formulas

Revise the Concepts of Chemical Energetics completely & thoroughly to solve the related problems at a faster pace. You can develop deeper knowledge on the fundamentals of Chemical Energetics after going through the formulae list compiled over here. Solve numerous problems so that you can recall the Chemical Energetics Formulas simply rather than by hearting.

1. System:

• Open: [exchange matter and energy] with the surroundings.
• Closed: [exchanged only energy] with the surroundings.
• Isolated: [exchanged neither matter nor energy] with the surroundings.

2. E, Internal energy and ΔE:
E = E_t + E_v + E_r + E_e + E_n + E_p etc.
ΔE = E_p – E_R [R → P]

3. H₁ Enthalpy or heat content and ΔH:
ΔH = H_p – H_R [R → P]
ΔH = – ve (exothermic)
ΔH = +ve (endothermic)

4. Work and Heat (Sing convention):
☞ work done by the system is negative
☞ work done on the system is positive
☞ heat observed by the system is positive
☞ heat observed by the surroundings is negative

5. First Law:
ΔE = Q + W (SI)
ΔE = Q – W (non-SI)

6. Expression for pressure volume work:
W = -PΔV

7. Maximum work in a reversible expansion:
W = -2.303 n RT log \(\frac{V_{2}}{V_{1}}\)
= – 2.303 nRT log \(\frac{P_{1}}{P_{2}}\)
W_rev ≥ W_irr

8. Isothermal process:
ΔE = 0, ΔH = 0, Q = -W

9. Isochoric process:
W = 0, Q = ΔE

10. Adiabatic process:
Q = 0, ΔE = W

11. Cyclic process:
ΔE = 0
q = – W

12. Isothermal isobaric process:
= Q – W,
ΔE = 0, ΔH = 0

13. Adiabatic reversible expansion:
Tv^γ-1 = constant
PV^γ = constant [γ = \(\frac{C_{p}}{C_{v}}\)]

14. Enthalpy and heat content:
ΔH = ΔE + PΔV [q(p) = q (v) + Δn_gRT]
ΔH = ΔE + Δn_gRT [Δn_g = n_p – n_r]

15. Unit for heat (cal. and joule):
1 cal = 4.184 J
1 Lt-atm = 101.3 J = 24.206 cal

16. KirchofPs equation:
ΔE_T2 = ΔE_T1 + ΔC_V (T₂ – T₁) [constant V]
ΔH_T2 = ΔH_T1 + ΔC_P (T₂ – T₁) [constant P]

17. Entropy(s):
Measure of disorder or randomness
ΔS = ΣS_p – ΣS_R
ΔS = \(\frac{\mathrm{q}_{\mathrm{rev}}}{\mathrm{T}}\) = 2.303 nR log \(\frac{V_{2}}{V_{1}}\)
= 2.303 nR log \(\frac{P_{1}}{P_{2}}\)

18. Fusion process:
ΔS = \(\frac{\Delta \mathrm{H}_{\text {fus. }}}{\mathrm{T}_{\mathrm{f}}}\)
☞ Vapourisation process
ΔS = \(\frac{\Delta \mathrm{H}_{\mathrm{vap}}}{\mathrm{T}_{\mathrm{b}}}\)
☞ For reversible process:
ΔS_sys + ΔS_surr = 0
☞ For an irreversible process: ΔS_sys + ΔS_surr > 0

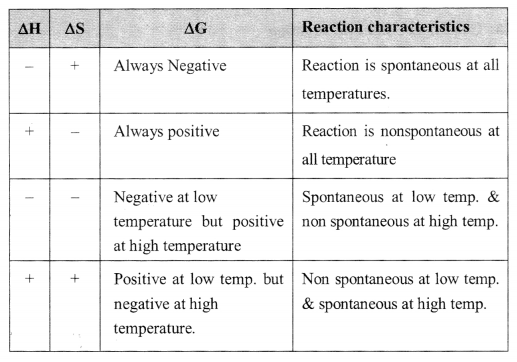
19. Free energy change:
ΔG = ΔH – TΔS
ΔG < 0 (spontaneous) [-ve] ΔG = 0 (equilibrium) ΔG > 0 (non-spontaneous) [+ve]
– ΔG is measure at useful work
– ΔG = W (maximum) – PΔV
☞ ΔG° = – 2.303 RT log K [K = equilibrium constant]

20. Clapeyron – Clausius equation|
log\(\frac{P_{2}}{P_{1}}=\frac{\Delta H_{v}}{2.303 R}\left(\frac{T_{2}-T_{1}}{T_{2} T_{1}}\right)\)
ΔH_V = Latent heat of vapourisation

21. Third law Lt T → 0, S = 0 [for a perfect crystalline substance]
☞ Carnot’s cycle (second law): Efficiency of heat engine:

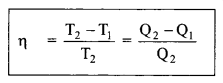
22. Different forms of heat of reaction:
Heat of combustion, heat of hydration, heat of neutralization, heat of fusion, heat of vapourisation, heat of sublimation etc.
(Enthalpy of reaction: R → P
ΔH° = ΣΔH°_r(P) – ΣΔH°_f(R_f)

23. Hess’s law: (Path-1)
ΔH = ΔH₁ + ΔH₂ (Path-II)

24. Heat of formation:
Change in heat content when one mole of the substance is formed from its element.
ΔH°₂₉₈ = H°_compound
[standard enthalpy of free element is taken as zero]

25. Hear of reaction from bond energy:
ΔH = [sum of BE of reactants] – [sum of BE of products]
☞ Bom Haber cycle is used to determine lattice energy.
☞ Heat capacity
C_p = \(\left(\frac{\partial \mathrm{H}}{\partial \mathrm{T}}\right)_{\mathrm{p}}\), C_v = \(\left(\frac{\partial \mathrm{E}}{\partial \mathrm{T}}\right)_{\mathrm{v}}\)
C_p – C_v = R [C_p > C_v]
γ = \(\frac{C_{p}}{C_{v}}\)
☞

Avail one-stop destination for formulae of different subjects from Onlinecalculator.guru and be thorough with the concepts.