Circular Motion Formulas
Circular Motion can be uniform as well as non-uniform. To help you learn the concept of Circular Motion better we have listed the Circular Motion Formulas in an efficient manner. Go through the Cheat Sheet of Circular Motion and be familiar with different sub-topics like Newton Equation in Circular Motion, Centripetal Force, Net Acceleration, etc. If you need help with more related concepts have a glance at our Physics Formulas and have a deeper insight into underlying concepts.
Cheat Sheet for Circular Motion
1. Circular motion
(a) angle(in radians) = \(\frac{\text { arc }}{\text { radius }}\)
or Δθ = \(\frac{\Delta \mathrm{S}}{\mathrm{r}}\) π rad. = 180°
(b) Angular velocity (\(\vec{\omega}\))
1. Instantaneous ω = \(\frac{d \theta}{d t}\)
2. Average \(\vec{\omega}_{\mathrm{av}}=\frac{\text { total angular displacement }}{\text { total time taken }}=\frac{\Delta \theta}{\Delta \mathrm{t}}\)
if v → linear velocity
α → angular acceleration
a → linear acceleration
(c) v = rω and \(\overrightarrow{\mathrm{v}}=\vec{\omega} \times \overrightarrow{\mathrm{r}}\)
(d) α = \(\frac{\mathrm{d} \vec{\omega}}{\mathrm{dt}}=\frac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}\) or α = ω\(\frac{\mathrm{d} \omega}{\mathrm{d} \theta}\)
(e) a = α r and \(\vec{a}=\vec{\alpha} \times \vec{r}\)
2. Newtons equation in circular motion
ω = ω0 + α t
θ = ω0 t + \(\frac{1}{2}\) α t2
ω2 = ω02 + 2 α θ
3. Centripetal force
Fc = \(\frac{m v^{2}}{r}\) = mω2r = mωv
ac = \(\frac{v^{2}}{r}\) In vector \(\overrightarrow{\mathrm{F}}_{\mathrm{c}}=\mathrm{m}(\vec{\omega} \times \overrightarrow{\mathrm{v}})\)
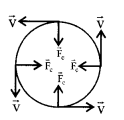
4. Net acceleration
\(\overrightarrow{\mathrm{a}}=\overrightarrow{\mathrm{a}}_{\mathrm{c}}+\overrightarrow{\mathrm{a}}_{\mathrm{t}}\)
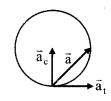
at → Tangential acceleration,
ac → Centripetal acceleration anct
anet = \(\sqrt{a_{t}^{2}+a_{c}^{2}}\)
ac = \(\frac{v^{2}}{r}\) = ω2r = vω; at = \(\frac{d v}{d t}=\frac{d^{2} r}{d t^{2}}=\frac{v d v}{d x}\) = rα
5. Motion in horizontal circle (conical pendulum)
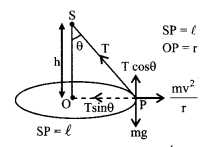
T cos θ = mg
T sin θ = mv2/r; tan θ = \(\frac{v^{2}}{r g}\)
tension T = mg \(\sqrt{1+\frac{v^{4}}{r^{2} g^{2}}}\)
The time period of revolution
T = \(2 \pi \sqrt{\frac{\mathrm{h}}{\mathrm{g}}}=2 \pi \sqrt{\frac{l \cos \theta}{\mathrm{g}}}\)
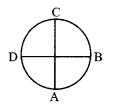
6. Vertical circular motion in case of string
(a) Tension at the lowest point A
TA = \(\frac{m v_{A}^{2}}{\ell}\) + mg
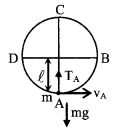
(b) Tension at point C
TC = \(\frac{m v_{C}^{2}}{\ell}\) – mg
TC = \(\frac{m v_{A}^{2}}{\ell}\) – 5 mg
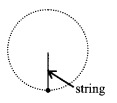
(c) Tension at point B
TB = \(\frac{m v_{B}^{2}}{\ell}\)
TB = \(\frac{m v_{A}^{2}}{\ell}\) – 2mg
TA – TC = 6mg
TA – TB = 3 mg
Thus TA > TB > TC
7. Critical velocity (vC)
The minimum velocity at which the circular motion is possible.
vC at A = \(\sqrt{5 \mathrm{g} \ell}\)
vC at C = \(\sqrt{g l}\)
vC at B = \(\sqrt{3 \mathrm{g} \ell}\)
In the case of a critical velocity
TA = 6mg
TC = 0
TB = 3mg
Case
⇒ If vA > \(\sqrt{5 \mathrm{g} \ell}\)
Tension in string never becomes zero, particle will continue the circular motion.
⇒ If vA = \(\sqrt{5 \mathrm{g} \ell}\)
Tension at point C becomes zero particle will just complete the circle.
⇒ If \(\sqrt{2 \mathrm{g} \ell}<\mathrm{v}_{\mathrm{A}}<\sqrt{5 \mathrm{g} \ell}\)
Particle will not follow circular motion, Tension becomes zero somewhere : between points B and C.
⇒ If vA = \(\sqrt{2 \mathrm{g} \ell}\)
Both velocity and tension becomes zero at B & D and particle will ! oscillate along semi-circular path.
⇒ If vA < \(\sqrt{5 \mathrm{g} \ell}\)
Velocity becomes zero between A & B but tension will not be zero any where. Particle oscillate about the point A.
8. Vertical circular motion in case of massless rod
Critical velocity
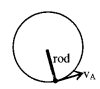
vC at A = \(\sqrt{4 \mathrm{g} \ell}\)
vC at C = 0
vC at B = \(\sqrt{2 \mathrm{g} \ell}\)
TA = 5 mg
TC = – mg
TB = 2 mg
9. Banking of tracks
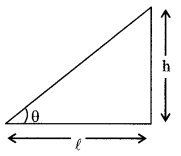
\(\frac{\mathrm{h}}{\ell}\) = tan θ = \(\frac{v^{2}}{r g}\), on frictionless road, banked by θ
Maximum speed for skidding, on circular unbanked road Vmax = \(\sqrt{\mu \mathrm{rg}}\)
You can witness plenty of concepts related to Physics not just Circular Motion from our site Onlinecalculator.guru during your preparation for quick help.