Defects of Images and Vision Formulas
Want to master the concept of Defects of Images and Vision? You have arrived at the right page where you find complete info on the concept and Defects of Images and Vision Formulas as well. Refer to the Formula Collection over here and get to know the underlying concepts too in an easy manner. You will find Formulas related to concepts Chromatic aberration, Condition of achromatism, etc. Not just this concept you can find anything related from the Physics Formulas list and enhance your subject knowledge.
Defects of Images and Vision Formulas List
1. Chromatic aberration
The difference between fv and fR is a measure of longitudinal chromatic ) aberration, (L.C.A.) i.e.
L.C.A. = fR – fv with df = fv – fr
As, \(\frac{1}{f}=(\mu-1)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)\)
\(-\frac{\mathrm{df}}{\mathrm{f}^{2}}=\mathrm{d} \mu\left(\frac{1}{\mathrm{R}_{1}}-\frac{1}{\mathrm{R}_{2}}\right)\)
\(-\frac{\mathrm{df}}{\mathrm{f}}=\frac{\mathrm{d} \mu}{\mu-1}=\omega\) as ω = \(\frac{\mathrm{d} \mu}{\mu-1}\)
L.C.A. = -df = ω f
Now as far as single lens neither f nor can be zero, we can not have a single lens free from chromatic aberration.
2. Condition of achromatism
\(\frac{\omega_{1}}{\mathrm{f}_{1}}+\frac{\omega_{2}}{\mathrm{f}_{2}}=0 \text { or } \frac{\omega_{1}}{\omega_{2}}=-\frac{\mathrm{f}_{1}}{\mathrm{f}_{2}}\)
3. Difect of vision
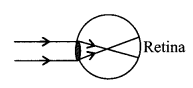
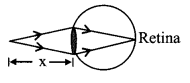
(i) Myopia or short sightedness
In this, distant objects are not clearly visible u = ∞, v = – x
power of lens P = \(\frac{1}{f}=\frac{1}{-x}\)
To overcome from this problem a concave lens is used.
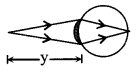
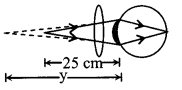
(ii) Hypermetropia or long sightedness:
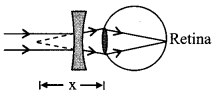
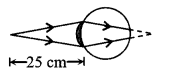
In this, near objects are not clearly visible
u = – 25 cm, v = – y
P = \(\frac{1}{f}=\frac{1}{25}-\frac{1}{y}\)
To overcome from this problem a convex lens is used.
(A)
(B)
(C)
Check out the go-to sheet for Formulas regarding various subjects like Physics, Chemistry, Maths all under one roof at Onlinecalculator.guru