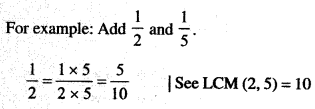Fractions Class 6 Maths Formulas
For those looking for help on Fractions Class 6 Math Concepts can find all of them here provided in a comprehensive manner. To make it easy for you we have jotted the Class 6 Fractions Maths Formulae List all at one place. You can find Formulas for all the topics lying within the Fractions Class 6 Fractions in detail and get a good grip on them. Revise the entire concepts in a smart way taking help of the Maths Formulas for Class 6 Fractions.
Maths Formulas for Class 6 Fractions
The List of Important Formulas for Class 6 Fractions is provided on this page. We have everything covered right from basic to advanced concepts in Fractions. Make the most out of the Maths Formulas for Class 6 prepared by subject experts and take your preparation to the next level. Access the Formula Sheet of Fractions Class 6 covering numerous concepts and use them to solve your Problems effortlessly.
A fraction is a number representing a part of a whole. The whole may be a single object or a group of objects. The other way round, we can say that a fraction is an operation on a number.
A Fraction
A fraction means a part of a group or of a region. \(\frac { 3 }{ 4 }\) is a fraction. We read it as “Three-fourths”.
Here, 4 stands for the number of equal parts into which the whole has been divided and 3 stands for the number of equal parts which have been taken out. It is to be noted that while expressing a situation of counting parts to write a fraction, all parts must be equal. Here, 3 is called the numerator and 4 is called the denominator. Numerator and denominator can be identified for any fraction.
Fractions can be represented on a number line. Any fraction has a point associated with it on the number line.
We know that a fraction essentially has a numerator and a denominator which can be identified for any fraction under consideration. If the numerator is less than the denominator, then the fraction is called a proper fraction.
For example:
\(\frac { 1 }{ 2 }\), \(\frac { 3 }{ 4 }\), \(\frac { 5 }{ 8 }\), \(\frac { 0 }{ 2 }\), etc.
A fraction, whose numerator is bigger than the denominator, is called an improper fraction.
For example: \(\frac { 5 }{ 4 }\), \(\frac { 7 }{ 2 }\), \(\frac { 11 }{ 3 }\), etc.
Improper fractions can be written as a combination of a whole and a part, and are then called mixed fractions.
For example: \(\frac { 5 }{ 4 }\) when written as 1\(\frac { 1 }{ 4 }\) is called a mixed fraction.
To express an improper fraction as a mixed fraction, we divide the numerator by denominator to get the quotient and the remainder. Then the mixed fraction can be written as
Quotient \(\frac { Remainder }{ Divisor }\)
To express a mixed fraction as an improper fraction, we multiply the whole with the denominator and add the numerator to it. Then the mixed fraction can be written as
\(\frac { (Whole\quad \times \quad Denominator)+Numerator }{ Denominator }\)
Two fractions are said to be equivalent if they represent the same quantity. Each proper or improper fraction has infinitely many equivalent fractions. To find an equivalent fraction of a given fraction, we multiply or divide both the numerator and the denominator of the given fraction by the same nonzero number. If two fractions are equivalent, then the product of the numerator of the first and the denominator of the second is equal to the product of the denominator of the first and the numerator of the second. This rule proves to be useful to find equivalent fractions.
The simplest form of a Fraction
A fraction is said to be in the simplest (or lowest) form if its numerator and denominator have no common factor except 1, i.e., they are coprime natural numbers. Thus, to find the equivalent fraction in the simplest form, we find the HCF of the numerator and the denominator. Then, we divide both of them by their HCF and get the equivalent fraction in the simplest form.
Like Fractions
Fractions, whose denominators are the same, are called like fractions.
For example: \(\frac { 1 }{ 9 }\), \(\frac { 4 }{ 9 }\), \(\frac { 7 }{ 9 }\) are all like fractions whereas \(\frac { 1 }{ 19 }\) and \(\frac { 1 }{ 20 }\) are not like fractions. The latter are called unlike fractions as their denominators are different.
Comparing Fractions
For fractions with the same numerators, the smaller the denominator, the greater the fraction.
For fractions with the same denominators, the greater the numerator, the greater the fraction.
Comparing like fractions
Since the like fractions are fractions with the same denominator, therefore, to compare two like fractions, it is just sufficient to compare their numerators. Greater the numerator, greater the fraction.
We know that in two fractions with the same denominator, one fraction with a bigger numerator is larger. Since in such cases the denominators are the same, i.e., these are like fractions, therefore only numerators are to be compared, so these comparisons are easy to make.
Comparing unlike fractions
We know that unlike fractions are fractions with different denominators. Now if their numerators are the same, then smaller the denominator, greater the fraction. However, if the two fractions have different numerators, then we find equivalent fractions of both and choose one from each such that their denominators are the same.
Then for comparison, greater the numerator, greater the fraction. Thus, we can find the greater of the two given fractions with different numerators and different denominators.
In daily life situations, sometimes we have to add two fractions and sometimes we have to subtract one from the other. This is respectively known as addition and subtraction of fractions.
An example of the addition of fractions is as follows:
Manish bought 2\(\frac { 1 }{ 2 }\) kg sugar whereas Preeti bought 1\(\frac { 1 }{ 2 }\) kg sugar. Find the total amount of sugar bought by them.
An example of subtraction of fractions is as follows:
The teacher taught \(\frac { 2 }{ 5 }\) of the book. Yash revised \(\frac { 2 }{ 5 }\) more on his own. How much does he still have to revise?
Adding or Subtracting like fractions
Addition of two or more like fractions can be carried out as follows:
Step 1. Add the numerators.
Step 2. Retain the denominator (common).
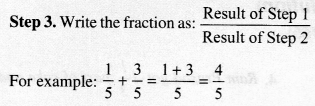
Subtraction of two fractions can be carried out as follows:
Step 1. Subtract the smaller numerator from the bigger numerator.
Step 2. Retain the denominator (common).
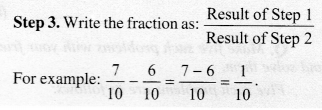
Adding and Subtracting Fractions
To add and subtract fractions that do not have the same denominator, we convert them into equivalent fractions with the same denominators and then proceed as above.