Gravitation Formulas
Have you ever wondered how to solve Gravitation Concept Related Problems easily? You can try out solving the Problems with our Gravitation Formulas List provided. Master the concept of Gravitation by accessing our Gravitation Cheat Sheet & Tables. Make your calculations at a faster pace rather than going with lengthy steps. Grab the opportunity and learn all the fundamentals of various physics concepts using the Physics Formulas provided.
Gravitation Formulae Sheet
1. Newton’s law of gravitation
F = \(\frac{\mathrm{Gm}_{1} \mathrm{m}_{2}}{\mathrm{r}^{2}}\)
G = 6.67 × 10-11 Nm2/kg2
\(\overrightarrow{\mathrm{F}}_{12}=-\overrightarrow{\mathrm{F}}_{21}\)
Always attraction in nature
2. Acceleration due to gravity
g = \(\frac{G M}{R^{2}}=\frac{4}{3}\)π GRρ
If M = const; g ∝ \(\frac{1}{R^{2}}\)
If ρ = const; g ∝ R
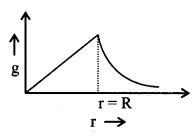
ρ → density of earth; M → mass of earth ; R → Radius of earth
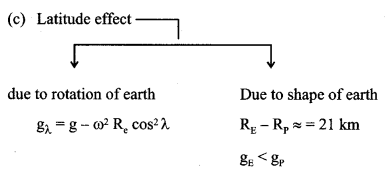
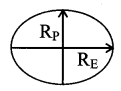
3. Variation of g
(a) Altitude (height) effect g’ = g \(\left(1+\frac{h}{R}\right)^{-2}\)
if h << R then g’ = g \(\left(1-\frac{2 h}{R}\right)\)
(b) effect of depth g” = g \(\left(1-\frac{\mathrm{d}}{\mathrm{R}}\right)\)
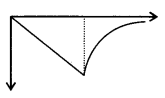
4. Intensity of gravitational field
\(\overrightarrow{\mathrm{E}}_{g}=\frac{\mathrm{GM}}{\mathrm{r}^{2}}(-\hat{\mathrm{r}})\)
for earth
Eg = g = 9.86 m/s2
| Solid | Hollow |
| 1. r > R, Eg = –\( \frac{\mathrm{GM}}{\mathrm{r}^{2}}\) | Eg = –\( \frac{\mathrm{GM}}{\mathrm{r}^{2}}\) |
| 2. r = R, Eg = –\( \frac{\mathrm{GM}}{\mathrm{R}^{2}}\) | Eg = –\( \frac{\mathrm{GM}}{\mathrm{R}^{2}}\) |
| 3. r < R, Eg = –\( \frac{\mathrm{GMr}}{\mathrm{R}^{3}} \) | Eg = 0 |
5. Gravitational potential due to solid sphere /hollow sphere
Vg = –\(\int_{\infty}^{r} \vec{E}_{g} \cdot \vec{d} r\)
For points out side (r > R)
Vg = –\(\frac{\mathrm{GM}}{\mathrm{r}}\), Vg = –\(\frac{\mathrm{GM}}{\mathrm{r}}\)
For points on the surface (r = R)
Vg = –\(\frac{\mathrm{GM}}{\mathrm{R}}\), Vg = –\(\frac{\mathrm{GM}}{\mathrm{R}}\)
For points inside it r < R
Vg = -GM\(\left[\frac{3 \mathrm{R}^{2}-\mathrm{r}^{2}}{2 \mathrm{R}^{3}}\right]\), Vg = –\(\frac{\mathrm{GM}}{\mathrm{R}}\)
6. Gravitational P.E.
Ug = mVg
Change in P.E. on Going height h above the surface
ΔUg = mgh if h << Re In general ΔUg = \(\frac{m g h}{\left(1+\frac{h}{R}\right)}\)
7. Orbital velocity of a satellite
\(\frac{m v_{o}^{2}}{r}=\frac{G M m}{r^{2}}\)
v0 = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}+\mathrm{h}}}\) (r = h + R)
if h << R
v0 = \(\sqrt{\frac{\mathrm{GM}}{\mathrm{R}}}=\sqrt{\mathrm{gR}}\) ≃ 8Km/sec.
8. Velocity of projection
loss of K.E. = gain in P.E.
\(\frac{1}{2} \mathrm{mv}_{\mathrm{p}}^{2}=-\frac{\mathrm{GMm}}{(\mathrm{R}+\mathrm{h})}-\left(-\frac{\mathrm{GMm}}{\mathrm{R}}\right)\)
vp = \(\left[\frac{2 \mathrm{GMh}}{\mathrm{R}(\mathrm{R}+\mathrm{h})}\right]^{1 / 2}=\left[\frac{2 \mathrm{gh}}{1+\frac{\mathrm{h}}{\mathrm{R}}}\right]^{1 / 2}\) (∵ GM = gR2)
9. Period of revolution
T = \(\frac{2 \pi r}{v_{0}}=\frac{2 \pi(R+h)^{3 / 2}}{R \sqrt{g}}\)
or T2 = \(\frac{4 \pi^{2} r^{3}}{G M}\)
If h << R
T = \(\frac{2 \pi R^{3 / 2}}{R \sqrt{g}} \simeq 1 \frac{1}{2}\) HR.
10. K.E. of satellite
K.E. = \(\frac{G M m}{2 r}=\frac{1}{2}\)mv02
11. P.E. of satellite
U = –\(\frac{\mathrm{GMm}}{\mathrm{r}}\)
12. Binding energy of satellite
BE = \(\frac{1}{2} \frac{\mathrm{GMm}}{\mathrm{r}}\)
13. Escape velocity
ve = \(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}=\sqrt{2 \mathrm{g} \mathrm{R}}=\mathrm{R} \sqrt{\frac{8 \pi \mathrm{Gd}}{3}}\)
ve = v0 \(\sqrt{2}\)
14. Effective weight in a satellite
W = 0
satellite behaves like a free fall body
15. Kepler’s laws for planetary motion
- Elliptical orbit with sun at one focus
- Areal velocity constant dA/dt = constant = \(\frac{L}{2 m}\)
- T2 ∝ r3, r = (r1 + r2)/2
Explore several physics concepts formulas all at one place i.e. Onlinecalculator.guru and make your calculations easier and at a faster pace comparatively.