Kinetic Theory of Gases Formulas
You may feel the concept of the Kinetic Theory of Gases difficult to understand. To help you out we have compiled the Kinetic Theory of Gases Formulas to make your job simple. Kinetic Theory of Gases Cheat Sheet will make it easy for you to get a good hold on the underlying concepts. The Formula Sheet & Tables provided covers various concepts like Mean Velocity, Mean Speed, Mean Square Velocity, Maxwell's Law, etc. For more information regarding several Physics Concepts check out Physics Formulas and lay a stronger foundation of basics.
Kinetic Theory of Gases Formulae Sheet
1. Gas laws
(i) Boyle’s laws
V ∝ \(\frac{1}{P}\) at constant temp. & mass.
PV = constant
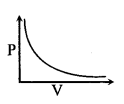
(ii) Charle’s law
V ∝ T, If m & P are constant
\(\frac{V}{T}\) = constant
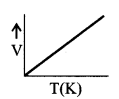
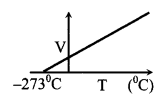
(iii) Gaylussac’s law
P ∝ T, if m & V are constant
\(\frac{V}{T}\) = constant
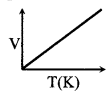
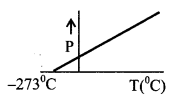
(iv) IDEAL GAS law ⇒
PV = nRT n → No. of moles.
PV = NkT N → Number of molecules
R = NAk NA → Avogadro No. = 6.02 × 1023 per gram / mole
2. Assumptions of kinetic theory of gases
a. A gas consist of a very large number of molecules which are perfect elastic spheres and are identical in all respects for a given gas and are different for different gases.
b. The molecules of a gas are in a state of continuous, rapid and random motion. They move in all directions with different speeds, ranging from zero to infinity and obey Newton’s laws of motion.
c. The size of the gas molecules is very small as compared to the distance between them. Hence volume occupied by the molecules is negligible in comparison to the volume of the gas
d. The molecules do not exert any force of attraction or repulsion on each other, except during collision.
e. The collisions of the molecules with themselves and with the walls of the vessel are perfectly elastic. As such the momentum and the kinetic energy of the molecules are conserved during collisions.
f. There is no concentration of the molecules at any point inside the container i.e. molecular density is uniform throughout the gas.
g. A. molecule moves along a straight line between two successive collisions and the average straight distance covered between two successive collisions is called the mean free path of the molecules.
h. The collisions are almost instantaneous, i.e. the time of collisions of two molecules is negligible as compared to time interval between two successive collisions.
3. Mean velocity
\(\overrightarrow{\mathrm{v}}=\frac{\overrightarrow{\mathrm{v}}_{1}+\overrightarrow{\mathrm{v}}_{2}+\ldots \ldots .+\overrightarrow{\mathrm{v}}_{\mathrm{n}}}{\mathrm{n}}=0\)4. Mean speed
\(\bar{v}=\frac{v_{1}+v_{2}+\ldots \ldots+v_{n}}{n} \neq 0\)
\(\overline{\mathrm{v}}=\sqrt{\frac{8 \mathrm{RT}}{\pi \mathrm{M}}}=\sqrt{\frac{8 \mathrm{kT}}{\pi \mathrm{m}}}\)
M is molecular weight and m is mass of a molecule.
5. Mean square velocity or mean square speed
\(\bar{v}^{2}=\frac{v_{1}^{2}+v_{2}^{2}+\ldots \ldots .+v_{n}^{2}}{n}\)6. Root mean square velocity (Vrms)
Square root of mean square velocity.
- vrms = \(\left(\bar{v}^{2}\right)^{1 / 2}=\sqrt{\frac{3 R T}{M}}=\sqrt{\frac{3 k T}{m}}\)
- vrms = \(\sqrt{\frac{3 \mathrm{P}}{\rho}}\)
- vrms ∝ \(\sqrt{T}\), \(\frac{1}{\sqrt{M}} \& \frac{1}{\sqrt{\rho}}\)
7. Maxwell’s law of distribution of speeds
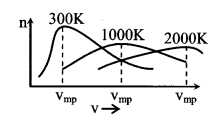
- Average speed \(\bar{v}=\sqrt{\frac{8 R T}{\pi M}}=\sqrt{\frac{8 k T}{\pi m}}=1.59 \sqrt{\frac{R T}{M}}\)
- Root mean square vrms = \(\sqrt{\frac{3 \mathrm{RT}}{\mathrm{M}}}=\sqrt{\frac{3 \mathrm{kT}}{\mathrm{m}}}=1.73 \sqrt{\frac{\mathrm{RT}}{\mathrm{M}}}\)
- Most probable speed vmp = \(\sqrt{\frac{2 \mathrm{RT}}{\mathrm{M}}}=\sqrt{\frac{2 \mathrm{kT}}{\mathrm{m}}}=1.41 \sqrt{\frac{\mathrm{RT}}{\mathrm{M}}}\)
vmp : \(\overline{\mathbf{v}}\) : vrms = 1.41 : 1.59 : 1.73
![]()
8. Pressure exerted by a gas
During their random motion molecules hit the walls of the container and impart momentum. The momentum imparted per second per unit area is pressure.
- P = \(\frac{1}{3}\left(\frac{\mathrm{mn}}{\mathrm{V}}\right) \overline{\mathrm{v}}^{2}=\frac{1}{3} \rho \mathrm{v}_{\mathrm{rms}}^{2}\)
- P = \(\frac{2}{3}\left(\frac{1}{2} \rho \bar{v}^{2}\right)=\frac{2}{3}\)E
E is mean kinetic energy per unit volume.
9. Interpretation of temperature
Temperature measures the mean kinetic energy of the molecules of gas.
\(\frac{1}{2} m \bar{v}^{2}=\frac{1}{2} m v_{r m s}^{2}=\frac{3}{2}\) kT (per molecule)
\(\frac{1}{2} M \bar{v}^{2}=\frac{3}{2}\) RT (per mole)
→ Kinetic energy per molecule = \(\frac{3}{2}\) kT
→ Kinetic energy per mole = \(\frac{3}{2}\) RT
→ Kinetic energy per gm = \(\frac{3}{2} \frac{R}{M}\) T
→ Kinetic energy per unit volume = \(\frac{1}{2} \rho \bar{v}^{2}=\frac{3}{2} P\)
10. Gramm’s law of diffusion
D ∝ \(\frac{1}{\sqrt{\rho}}\)
or
\(\frac{D_{1}}{D_{2}}=\sqrt{\frac{\rho_{2}}{\rho_{1}}}\)
11. Dalton’s law of partial pressures
It states that the total pressure exerted by a mixture of gases which do not interact with one another, is equal to sum of the partial pressures which each would exert, if it alone occupied the same volume at the given temperature
P = P1 + P2 + …….. + Pn
12. Vander wall’s gas equation
\(\left(P+\frac{a}{V^{2}}\right)\) (V – b) = RT (for one mole)
\(\frac{\mathrm{a}}{\mathrm{V}^{2}}\) is correction in pressure due to attraction between the molecules and b is correction in volume due to finite size of molecules.
For n-mole gas \(\left[\mathrm{P}+\mathrm{a}\left(\frac{\mathrm{n}}{\mathrm{V}}\right)^{2}\right]\)[V – nb] = nRT
13. Critical constants
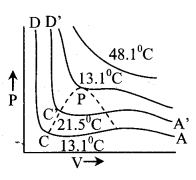
Pc = \(\frac{a}{27 b^{2}}\), Vc = 3b
and Tc = \(\frac{8 \mathrm{a}}{27 \mathrm{Rb}}\)
\(\frac{P_{c} V_{c}}{R T_{c}}=\frac{3}{8}\) (for real gas)
14. Mean free path
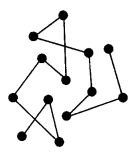
The straight line path traversed between two collisions is called free path. The mean of these two collisions is called free path.
The mean of these paths is mean free path \(\bar{\lambda}\).
\(\bar{\lambda}=\frac{1}{\sqrt{2} \pi \mathrm{d}^{2} \mathrm{n}}=\frac{\mathrm{k} \mathrm{T}}{\sqrt{2} \pi \mathrm{d}^{2} \mathrm{P}}\)
d is diameter of molecules and n is number of molecule per unit volume.
P → pressure, T → temperature (In Kelvin)
15. Degree of freedom
The number of independent variables required to describe the state of | system is its degrees of freedom. For molecules generally these can be translational, rotational and vibration. For a molecule the number of degree of freedom f = 3N – B.
N → Number of atoms in the molecule and B is number of bonds or restraints.
Monatomic gas:
N = 1, B = 0, f = 3 (translational)
Diatomic gas: Molecule dumb-bell shaped,
N = 2, B = 1, f = 5 (3 translational + 2 rotational)
Triatomic gas: Linear molecules (CO2),
N = 3,B = 2, f = 7(3 translational + 2 rotational + 2 vibrationally)
Non-linear molecules (H2O),
N = 3,B = 3, f = 6(3 translational + 3rotational)
16. Maxwell’s law of equipartition of energy
Total energy is equally divided among the various degrees of freedom. Mean energy for each degree of freedom per molecule = \(\frac{1}{2}\) kT.
For f degrees of freedom mean energy per molecule = \(\frac{1}{2}\) fkT.
Mean energy per mole E = \(\frac{1}{2}\) NfkT (Nk = R)
= \(\frac{1}{2}\) fRT
For n-moles mean energy = \(\frac{1}{2}\) nfRT
17. SPECIFIC HEATS OF GAS
(i) Specific heat at constant volume Cv (Molar heat capacity)
Cv = \(\left(\frac{d E}{d T}\right)_{v}=\frac{d}{d T}\left(\frac{1}{2} f R T\right)=\frac{1}{2}\)fR
Cv = \(\frac{3}{2}\) R (Monatomic gas)
Cv = \(\frac{5}{2}\) R (Diatomic gas)
(ii) Specific heat at constant pressure Cp –
Cp = Cv + R
= \(\left(\frac{1}{2} f+1\right)\)R
Cp – Cv = R (Mayer’s relation)
Cp = \(\frac{5}{2}\) R (Monatomic gas)
Cp = \(\frac{7}{2}\) R (Diatomic gas)
(iii) Ratio of specific heats of a gas (γ)
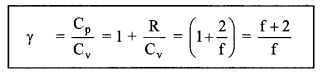
γ = \(\frac{5}{3}\) = 1.67 (monatomic gas)
γ = \(\frac{7}{5}\) = 1.40 (Diatomic gas)
γ = decreases with increase of atomicity.
18. Mixture of non-reacting gases
(i) Mole fraction n = n1 + n2
(ii) Eq. Molecular weight
M = \(\frac{\mathrm{n}_{1} \mathrm{M}_{1}+\mathrm{n}_{2} \mathrm{M}_{2}}{\mathrm{n}_{1}+\mathrm{n}_{2}}\)
(iii) Eq. Specific heat
Cv = \(\frac{\mathrm{n}_{\mathrm{I}} \mathrm{C}_{\mathrm{v}_{1}}+\mathrm{n}_{2} \mathrm{C}_{\mathrm{v}_{2}}}{\mathrm{n}_{1}+\mathrm{n}_{2}}\)
Cp = \(\frac{\mathrm{n}_{1} \mathrm{C}_{\mathrm{P}_{1}}+\mathrm{n}_{2} \mathrm{C}_{\mathrm{p}_{2}}}{\mathrm{n}_{1}+\mathrm{n}_{2}}\)
(iv) Final Temperature
T = \(\frac{N_{1} T_{1}+N_{2} T_{2}}{N_{1}+N_{2}}=\frac{n_{1} T_{1}+n_{2} T_{2}}{n_{1}+n_{2}}\)
N1 = n1NA, N2 = n2NA
NA is Avogadro’s number.
(v) Eq. γ = \(\frac{\mathrm{n}_{1} \mathrm{C}_{\mathrm{P}_{1}}+\mathrm{n}_{2} \mathrm{C}_{\mathrm{P}_{2}}}{\mathrm{n}_{1} \mathrm{C}_{\mathrm{v}_{1}}+\mathrm{n}_{2} \mathrm{C}_{\mathrm{v}_{2}}}\)
Explore more concepts of Physics and understand them easily taking the help of the Formulas Collection existing at Onlinecalculator.guru and get a good grip on them.