Laws of Conservation Formulas
If you are in search of the Law of Conservation Formulas then you have come the right way as we have listed all of them here. The main motto behind providing the Law of Conservation Formulae List is to simplify your work. Try to apply these Formulas during your calculations and arrive at the solutions easily. The Formula Sheet of Laws of Conservation includes formulas for direct elastic collision, head on inelastic collision, oblique collision, etc. For instant help regarding the concepts of Physics have a look at the Physics Formulas provided.
Important Laws of Conservation Formulae
If \(\overrightarrow{\mathrm{F}}=\mathrm{F}_{\mathrm{x}} \hat{\mathrm{i}}+\hat{\mathrm{i}} \text { Fy } \hat{\mathrm{i}}+\mathrm{F}_{\mathrm{z}} \hat{\mathrm{k}}\)
& \(\overrightarrow{\mathrm{P}}=\mathrm{P}_{\mathrm{x}} \hat{\mathrm{i}}+\hat{\mathrm{i}} \text { Py } \hat{\mathrm{i}}+\mathrm{P}_{\mathrm{z}} \hat{\mathrm{k}}\)
Fx = \(\frac{\mathrm{dP}_{\mathrm{x}}}{\mathrm{dt}}\) if Fx = 0 , then Px = constant
Fy = \(\frac{\mathrm{dP}_{\mathrm{y}}}{\mathrm{dt}}\) if Fy = 0, then Py = constant
Fz = \(\frac{\mathrm{dP}_{\mathrm{z}}}{\mathrm{dt}}\) if Fz = 0, then Pz = constant
1. Important formula and features for direct elastic collision / head on elastic collision in id
(i) The velocity of first body after collision
v1 = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right) u_{1}+\left(\frac{2 m_{2}}{m_{1}+m_{2}}\right)\)u2
(ii) The velocity of second body after collision
v2 = \(\left(\frac{2 m_{1}}{m_{1}+m_{2}}\right) u_{1}+\left(\frac{m_{2}-m_{1}}{m_{1}+m_{2}}\right)\)u2
(iii) If the body with mass m2 is initially at rest i.e. u2 = 0
v1 = \(\left(\frac{m_{1}-m_{2}}{m_{1}+m_{2}}\right)\)u1
and v2 = \(\left(\frac{2 m_{1}}{m_{1}+m_{2}}\right)\)u1
(iv) When a particle of mass m1 moving with velocity u1, collides with another particle with m2 at rest and if.
m1 = m2 m1 >> m2 m1 << m2
⇒ v1 = 0 ⇒ v1 = u1 ⇒ v1 = -u1
and v2 = u1 and v2 = 2u1 and v2 = \(\frac{2 m_{1}}{m_{2}}\)u1 ≈ 0
(v) When m1 = m2 = m but u2 ≠ 0, then v1 = u2 and v2 = u1 i.e. the particles mutually exchange their velocities.
(vi) Exchange of energy is maximum when m1 = m2. This fact is utilized in atomic reactor in slowing down the neutrons. To slow down the neutrons, these are made to collide with nuclei of almost similar mass. For this hydrogen nuclei are most appropriate.
2. Head on inelastic collision
(a) In this case Total momentum before collision = Total momentum after collision
⇒ \(\mathbf{m}_{1} \overrightarrow{\mathbf{u}}_{1}+\mathbf{m}_{2} \overrightarrow{\mathbf{u}}_{2}=\mathbf{m}_{1} \overrightarrow{\mathbf{v}}_{1}+\mathbf{m}_{2} \overrightarrow{\mathbf{v}}_{2}\)
but K.E.b.c. ≠ K.E.a.c.
⇒ K.E.b.c. = K.E.a.c. + Q
where Q = heat energy, sound energy etc.
⇒ \(\frac{1}{2}\) m1u12 + \(\frac{1}{2}\) m2u22 > \(\frac{1}{2}\) m1v12 + \(\frac{1}{2}\) m2v22
(b) According to Newton’s law, for inelastic collision we have
\(\overrightarrow{\mathrm{v}}_{1}-\overrightarrow{\mathrm{v}}_{2}=-\mathrm{e}\left(\overrightarrow{\mathrm{u}}_{1}-\overrightarrow{\mathrm{u}}_{2}\right)\)
(c) In inelastic collision, velocity of first body after collision
v1 = \(\left(\frac{m_{1}-e m_{2}}{m_{1}+m_{2}}\right) u_{1}+\frac{m_{2}(1+e)}{m_{1}+m_{2}} u_{2}\)
and v2 = \(\frac{m_{1}(1+e)}{m_{1}+m_{2}} u_{1}+\frac{m_{2}-e m_{1}}{m_{1}+m_{2}} u_{2}\)
(d) Loss of energy in inelastic collision
ΔEk = \(\frac{1}{2}\left(\frac{m_{1} m_{2}}{m_{1}+m_{2}}\right)\)(u1 – u2)2(1 – e2)
(e) Important Results:
(i) If e = 0 (perfect inelastic)
v1 = v2 = \(\frac{\mathrm{m}_{1} \mathrm{u}_{1}+\mathrm{m}_{2} \mathrm{u}_{2}}{\mathrm{m}_{1}+\mathrm{m}_{2}}\)
ΔEk = \(\frac{1}{2} \frac{m_{1} m_{2}}{m_{1}+m_{2}}\)(u1 – u2)2
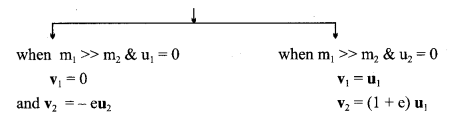
(ii) if m1 >> m2
then v1 ≃ u1,
v1 ≃ (1 + e)u1 – eu2
3. Oblique collision
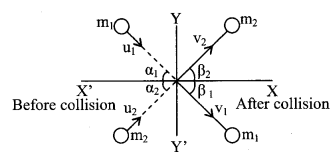
(a) Applying law of conservation of linear momentum along X axis
(Px)b.c. =(Px)a.c.
⇒ m1u1 cos α1 + m2u2 cos α2= m1v1 cos β1 + m2v2 cos β1 and along y-axis
(Py)b.c. =(Py)a.c.
⇒ m1u1 sin α1 + m2u2 sin α2= m1v1 sin β1 + m2v2 sin β1
(b) Applying law of conservation of K.E.
(K.E.)b.c. = (K.E.)a.c.
⇒ \(\frac{1}{2} \mathrm{m}_{1} \mathrm{u}_{1}^{2}+\frac{1}{2} \mathrm{m}_{2} \mathrm{u}_{2}^{2}=\frac{1}{2} \mathrm{m}_{1} \mathrm{v}_{1}^{2}+\frac{1}{2} \mathrm{m}_{2} \mathrm{v}_{2}^{2}\)
(c) If m1 = m2 and (α1 + α2) = 90°, (β1 + β2) = 90° which means if two particles of same mass moving at right angles to each other collide elastically, after collision they move at right angles to each other.
(d) If a body A collides elastically with another body B of same mass at rest at a glancing angle, then after collision the two bodies move at right angle to each other.
Feel the extremely difficult concepts that you never seemed to understand too easily with the formulas curated for various concepts on Onlinecalculator.guru