Magnetic Effect of Current Formulas

1. Biot-savart’s law

The magnetic field at a certain point due to an element δl of a current-carrying conductor is

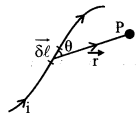
δB = \(\frac{\mu_{0}}{4 \pi} \frac{i \delta \ell \sin \theta}{r^{2}}\)
or \(\overrightarrow{\mathrm{d} \mathrm{B}}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{i} \delta \vec{\ell} \times \hat{\mathrm{r}}}{\mathrm{r}^{2}}\)
= \(\frac{\mu_{0}}{4 \pi} \frac{i \delta \vec{\ell} \times \vec{r}}{r^{3}}\)
δ\(\overrightarrow{\mathrm{B}}\) is in a direction normal to the plane of δ\(\vec{\ell} \text { and } \vec{r}\)

2. Magnetic field due to a current caryying circular coil

(a) At the centre
B₀ = \(\frac{\mu_{0} \mathrm{ni}}{2 \mathrm{R}}\) along the axis of coil.

(b) At a point on the axis of a coil
B = \(\frac{\mu_{0} n i R^{2}}{2\left(R^{2}+x^{2}\right)^{3 / 2}}\)

(c) If x > > R, then
B = \(\frac{\mu_{0} \mathrm{niR}^{2}}{2 \mathrm{x}^{3}}\)

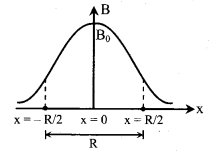
(d) At the point of inflexion, \(\frac{\mathrm{dB}}{\mathrm{dx}}\) = constant or \(\frac{d^{2} B}{d x^{2}}\) inflection are found in the field of a coil at x = ± R/2 and the distance between them is equal to the radius of the coil.

3. Magnetic field due to a current carrying straight wire of finite length

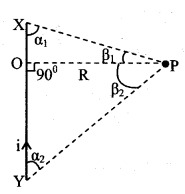
B = \(\frac{\mu_{0} \mathrm{i}}{4 \pi \mathrm{R}}\) (sin β₁ + sin β₂)
or B = \(\frac{\mu_{0} \mathrm{i}}{4 \pi \mathrm{R}}\) (cos α₁ + cos α₂)

4. Magnetising field (\(\overrightarrow{\mathrm{H}}\))

\(\overrightarrow{\mathrm{H}}=\overrightarrow{\mathrm{B}} / \mu_{0}\)

5. Ampere’s law

(a) The line integral of magnetic field along the closed path = p0 multiple of net current passing through that closed path
\(\oint \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \vec{\ell}=\mu_{0} \Sigma \mathrm{I}\)

(b) Magnetomotive force
F_m = \(\oint \overrightarrow{\mathrm{H}} \cdot \mathrm{d} \vec{\ell}=\frac{1}{\mu} \oint \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \vec{\ell}\)

6. Magnetic field due to a current carrying straight wire of infinite length

B = \(\frac{\mu_{0} i}{2 \pi r}=\frac{\mu_{0}}{4 \pi} \frac{2 i}{r}\)

7. Magnetic field due to a current carrying long and straight solid cylinder

• At a point out side the cylinder B_out = \(\frac{\mu_{0} i}{2 \pi r}\)
• At the surface B_surface = \(\frac{\mu_{0} i}{2 \pi R}\)
• At a point inside the cylinder B_in = \(\frac{\mu_{0} \mathrm{ir}}{2 \pi \mathrm{R}^{2}}\) ; R → Radius of cylinder.

8. Magnetic field due to a current carrying long and straight hollow cylinder

(a) At a point out side the cylinder
B_out = \(\frac{\mu_{0} i}{2 \pi r}\)

9. Magnetic behaviour of current carrying coil and its magnetic moment

• A small current carrying coil behaves like a small magnet.
• Magnetic moment of a current carrying coil

M = current × effective area.
For a coil of N turns
M = NiA = NiπR²

10. Current and magnetic field due to circular motion of charge

(a) Current i = ef = \(\frac{\mathrm{e}}{\mathrm{T}}\)
f → revolution/second, T → Time period
i = \(\frac{\mathrm{e} \omega}{2 \pi}=\frac{\mathrm{ev}}{2 \pi \mathrm{R}}\)

(b) Magnetic field B₀ = \(\frac{\mu_{0} n I}{2 R}=\frac{\mu_{0} n e f}{2 R}=\frac{\mu_{0} n e}{2 R T}\)
B₀ = \(\frac{\mu_{0} \text { ne } \omega}{4 \pi R}=\frac{\mu_{0} \text { nev }}{4 \pi R^{2}}\) (e → charge of electron)

(c) Magnetic moment
M = iA = efπR² = \(\frac{\mathrm{e} \pi \mathrm{R}^{2}}{\mathrm{T}}\)
M = \(\frac{\mathrm{e} \omega \mathrm{R}^{2}}{2}=\frac{\mathrm{evR}}{2}=\frac{\mathrm{eL}}{2 \mathrm{m}}\)
L → angular momentum, m → mass of electron

11. Force on a current carrying condcutor due to magnetic field

\(\overrightarrow{\mathrm{F}}=\mathrm{i}(\vec{\ell} \times \overrightarrow{\mathrm{B}})\)
\(|\overrightarrow{\mathrm{F}}|\) = i l B sin θ
Two parallel conductors carrying currents in the same direction attract each other but with currents in opposite direction repel each other.

12. Magnetic force between two parallel current-carrying conductors

Attractive or repulsive force on unit length of conductors
\(\frac{F}{\ell}=\frac{\mu_{0} i_{1} i_{2}}{2 \pi d}\)
d → distance between parallel conductors.

13. Motion of charged particle in a magnetic field

(a) Force on the particle
\(\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})\)
\(|\overrightarrow{\mathrm{F}}|\) = qvB sin θ

(b) when θ = 90°, the motion of particle will be along a circular path. Radius of circular path
R = \(\frac{m v}{q B}=\frac{\sqrt{2 m E}}{q B}=\frac{\sqrt{2 m q V}}{q B}\)
Period of revolution of the particle
T = \(\frac{2 \pi \mathrm{m}}{\mathrm{qB}}\)
Frequency of revolution
f = \(\frac{1}{\mathrm{T}}=\frac{\mathrm{qB}}{2 \pi \mathrm{m}}\)
Kinetic energy of the particle
E = \(\frac{\mathrm{R}^{2} \mathrm{q}^{2} \mathrm{B}^{2}}{2 \mathrm{m}}\)

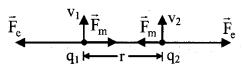
14. Interaction between two moving charges

(a) Magnetic field due to charge moving with velocity \(\overrightarrow{\mathrm{v}}\)
\(\overrightarrow{\mathrm{B}}=\frac{\mu_{0}}{4 \pi} \frac{\mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{r}})}{\mathrm{r}^{3}}\)
Hence B = \(\frac{\mu_{0}}{4 \pi} \frac{q v \sin \theta}{r^{2}}\)

(b) The electric and magnetic forces both act between moving charges.

(c) Electric force F_e = \(\frac{1}{4 \pi \epsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)

(d) Magnetic force F_m = \(\frac{\mu_{0}}{4 \pi} \frac{\mathrm{q}_{1} \mathrm{q}_{2} \mathrm{v}_{1} \mathrm{v}_{2}}{\mathrm{r}^{2}}\)
If v₁ = v₂ = v
then F_m = \(\frac{\mu_{0}}{4 \pi} \frac{q_{1} q_{2}}{r^{2}} v^{2}\)

(e) \(\frac{F_{m}}{F_{e}}=\frac{v^{2}}{c^{2}}=\left(\frac{v}{c}\right)^{2}\)
Stationary Charges:

Moving Charges:

15. Force and torque on a current-carrying coil placed in a uniform magnetic field

(a) resultant force F_net = 0.

(b) A torque acts on the coil
τ = iNAB sin θ = MB sin θ
M → magnetic dipole moment.
In vector form
τ = \(\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\)

(c) The work done in turning a loop from angle θ₁ to θ₂.
W = MB (cos θ₁ – cos θ₂)

(d) Time period of oscillation of a magnetic dipole in uniform M.F.
T = 2π\(\sqrt{\frac{\mathrm{I}}{\mathrm{MB}}}\); I → moment of inertia

Get instant help regarding formulas of various concepts from Physics all at one place on Onlinecalculator.guru a trusted and reliable portal.