Magnetism Formulas
You will never feel the concept of Magnetism difficult after referring to our Magnetism Formulas List. Have a quick look at the Magnetism Formulae Sheet and clear all your ambiguities regarding the particular concept. Start grasping the Magnetism Cheat Sheet provided and understand the concept behind them easily. You can get Formulas related to Magnetic Susceptibility, Magnetic Permeability, Hysteresis Loop from the further modules. Seek help on Magnetism or any other random topic of Physics using the Physics Formulas Collection of ours.
List of Magnetism Formulas
1. Magnetic moment
(a) The magnetic moment produced due to motion of electron:
M = iA = – \(\frac{\mathrm{ev}}{2 \pi \mathrm{r}}\) (πr2) = – \(\frac{\mathrm{evr}}{2}=-\frac{\mathrm{e} \omega \mathrm{r}^{2}}{2}\)
= \(\frac{\mathrm{e}}{2 \mathrm{m}}\)L = -n\(\left(\frac{\mathrm{eh}}{2 \pi \mathrm{m}}\right)\),
Here µB = \(\frac{\mathrm{eh}}{2 \pi \mathrm{m}}\) Bohr’s magneton
where L is the angular momentum of the electron,
(b) For a bar magnet
M = m × 2l
where m is the pole strength of the magnet.
2. Magnetic field due to a bar magnet
On the point of axis
B = \(\frac{\mu_{0} 2 \mathrm{Mr}}{4 \pi\left(\mathrm{r}^{2}-\ell^{2}\right)^{2}}\)
B ≈ \(\frac{\mu_{0}}{4 \pi} \frac{2 M}{r^{3}}\) (when r >> l)
On the point of equatorial
B = \(\frac{\mu_{0}}{4 \pi} \frac{M}{\left(r^{2}+\ell^{2}\right)^{3 / 2}}\)
B = \(\frac{\mu_{0}}{4 \pi} \frac{M}{r^{3}}\) when r >> l
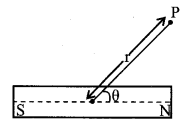
At a general point
3. Intensity of magnetisation (\(\overrightarrow{\mathrm{I}}\))
The magnetic moment induced per unit volume of the substance is intensity of magnetisation.
(a) I = \(\frac{M}{V}\) A/m
(b) I = \(\frac{m}{A}\)
A → cross sectional area; m → pole strength
4. Magnetic susceptibility (χ)
I ∝ H
I = χH
or χ = \(\frac{1}{\mathrm{H}}\) unitless quantity.
5. Magnetic permeability (µ)
i.e., µ = \(\frac{B}{H}\)
For vacuum µ0 = \(\frac{\mathrm{B}_{0}}{\mathrm{H}}\) = 4π × 10-7 H/m
Relative magnetic permeability
µr = \(\frac{\mu}{\mu_{0}}\)
6. Relations amongst B, H, I, χ AND µ
- B = µH = B0 + µ0I = µ0(H + I)
- B = µ0H(l + χ)
- µ = µ0(1 + χ)
- µr = (1 + χ)
7. Magnetic hysterisis loop, B-H or I-H curve
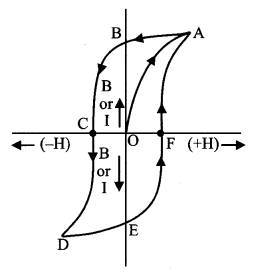
- B always lags behind H. This property is called magnetic hysterics.
- The curve drawn between B and H is called B-H curve. It is a closed curve for one complete cycle of magnetisation and demagnetisation.
- Hysterisis loss per cycle per unit volume = area bound by the hysterics loop.
8. Types of magnetic materials
- Diamagnetic material (µ < 1)
- Paramagnetic material (µ > l)
- Ferromagnetic material (µ >> 1)
9. Curie’s law and curie temperature
(a) For a paramagnetic material
χ ∝ \(\frac{1}{T}\) or χ = \(\frac{C}{T}\)
(b) For a ferromagnetic material
χ = \(\frac{C}{\left(T-T_{c}\right)}\)
where TC is curie temperature.
(c) The temperature at or above which the ferromagnetic material behaves like a paramagnetic material is called Curie temperature.
10. Terrestrial magnetism
Deals with the magnetic field of earth. It is described in terms of three quantities, which are called magnetic elements of earth. These are:
(i) Magnetic declination (θ) at a place is the angle θ between magnetic axis and the geographic axis. It is also equal to the angle between magnetic meridian and geographic merdian at the place
(ii) Magnetic Inclination or dip at a place is defined as the angle δ, which the direction of total intensity of earth’s magnetic field, (B) makes with a horizontal line in magnetic meridian.
(iii) Horizontal component, H is the component of total intensity of earth’s magnetic field (B) in the horizontal direction in magnetic meridian,
H = B cos δ
V = B sin δ
∴ \(\sqrt{H^{2}+V^{2}}\) = B
and \(\frac{V}{H}\) = tan δ
If you are looking for a place where you can find formulae for different concepts then Onlinecalculator.guru can be a great place for all your concerns.