MCQ Questions for Class 10 Maths Chapter 1 Real Numbers
MCQ Questions for Class 10 Maths Chapter 1 Real Numbers PDF Download
1. The decimal form of \(\frac{129}{2^{2} 5^{7} 7^{5}}\) is
(a) terminating
(b) non-termining
(c) non-terminating non-repeating
(d) none of the above
Answer
Answer: c
- Area Related to Circles Class 10 Formulas
- Surface Areas and Volumes Class 10 Formulas
- Constructions Class 10 Formulas
- Circles Class 10 Formulas
- Introduction to Trigonometry Class 10 Formulas
- Coordinate Geometry Class 10 Formulas
- Arithmetic Progression Class 10 Formulas
- Quadratic Equations Class 10 Formulas
- Pair Of Linear Equations in Two Variables Class 10 Formulas
- Polynomials Class 10 Formulas
- Real Numbers Class 10 Formulas
- Triangles Class 10 Formulas
- Some Applications of Trigonometry Class 10 Formulas
- Statistics Class 10 Formulas
- Probability Class 10 Formulas
2. HCF of 8, 9, 25 is
(a) 8
(b) 9
(c) 25
(d) 1
Answer
Answer: d
3. Which of the following is not irrational?
(a) (2 – √3)2
(b) (√2 + √3)2
(c) (√2 -√3)(√2 + √3)
(d)\(\frac{2 \sqrt{7}}{7}\)
Answer
Answer: c
4. The product of a rational and irrational number is
(a) rational
(b) irrational
(c) both of above
(d) none of above
Answer
Answer: b
5. The sum of a rational and irrational number is
(a) rational
(b) irrational
(c) both of above
(d) none of above
Answer
Answer: b
6. The product of two different irrational numbers is always
(a) rational
(b) irrational
(c) both of above
(d) none of above
Answer
Answer: b
7. The sum of two irrational numbers is always
(a) irrational
(b) rational
(c) rational or irrational
(d) one
Answer
Answer: a
8. If b = 3, then any integer can be expressed as a =
(a) 3q, 3q+ 1, 3q + 2
(b) 3q
(c) none of the above
(d) 3q+ 1
Answer
Answer: a
9. The product of three consecutive positive integers is divisible by
(a) 4
(b) 6
(c) no common factor
(d) only 1
Answer
Answer: b
10. The set A = {0,1, 2, 3, 4, …} represents the set of
(a) whole numbers
(b) integers
(c) natural numbers
(d) even numbers
Answer
Answer: a
11. Which number is divisible by 11?
(a) 1516
(b) 1452
(c) 1011
(d) 1121
Answer
Answer: b
12. LCM of the given number ‘x’ and ‘y’ where y is a multiple of ‘x’ is given by
(a) x
(b) y
(c) xy
(d) \(\frac{x}{y}\)
Answer
Answer: b
13. The largest number that will divide 398,436 and 542 leaving remainders 7,11 and 15 respectively is
(a) 17
(b) 11
(c) 34
(d) 45
Answer/ Explanation
Answer: a
Explaination:(a); [Hint. Algorithm 398 – 7 – 391; 436 – 11 = 425; 542 – 15 = 527; HCF of 391, 425, 527 = 17]
14. There are 312, 260 and 156 students in class X, XI and XII respectively. Buses are to be hired to take these students to a picnic. Find the maximum number of students who can sit in a bus if each bus takes equal number of students
(a) 52
(b) 56
(c) 48
(d) 63
Answer/ Explanation
Answer: a
Explaination:(a); [Hint. HCF of 312, 260, 156 = 52]
15. There is a circular path around a sports field. Priya takes 18 minutes to drive one round of the field. Harish takes 12 minutes. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet ?
(a) 36 minutes
(b) 18 minutes
(c) 6 minutes
(d) They will not meet
Answer/ Explanation
Answer: a
Explaination:(a); [Hint. LCM of 18 and 12 = 36]
16. Express 98 as a product of its primes
(a) 2² × 7
(b) 2² × 7²
(c) 2 × 7²
(d) 23 × 7
Answer
Answer: c
17. Three farmers have 490 kg, 588 kg and 882 kg of wheat respectively. Find the maximum capacity of a bag so that the wheat can be packed in exact number of bags.
(a) 98 kg
(b) 290 kg
(c) 200 kg
(d) 350 kg
Answer/ Explanation
Answer: a
Explaination:(a); [Hint. HCF of 490, 588, 882 = 98 kg]
18. For some integer p, every even integer is of the form
(a) 2p + 1
(b) 2p
(c) p + 1
(d) p
Answer
Answer: b
19. For some integer p, every odd integer is of the form
(a) 2p + 1
(b) 2p
(c) p + 1
(d) p
Answer
Answer: a
20. m² – 1 is divisible by 8, if m is
(a) an even integer
(b) an odd integer
(c) a natural number
(d) a whole number
Answer
Answer: b
21. If two positive integers A and B can be ex-pressed as A = xy3 and B = xiy2z; x, y being prime numbers, the LCM (A, B) is
(a) xy²
(b) x4y²z
(c) x4y3
(d) x4y3z
Answer
Answer: d
22. The product of a non-zero rational and an irrational number is
(a) always rational
(b) rational or irrational
(c) always irrational
(d) zero
Answer
Answer: c
23. If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is
(a) xy²
(b) x4y²z
(c) x4y3
(d) x4y3z
Answer
Answer: a
24. The largest number which divides 60 and 75, leaving remainders 8 and 10 respectively, is
(a) 260
(b) 75
(c) 65
(d) 13
Answer
Answer: d
25. The least number that is divisible by all the numbers from 1 to 5 (both inclusive) is
(a) 5
(b) 60
(c) 20
(d) 100
Answer
Answer: b
Explaination:(b); [Hint. LCM of 2, 3, 4, 5 = 60
26. The least number that is divisible by all the numbers from 1 to 8 (both inclusive) is
(a) 840
(b) 2520
(c) 8
(d) 420
Answer
Answer: a
27. The decimal expansion of the rational number \(\frac{14587}{250}\) will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Answer
Answer: c
28. The decimal expansion of the rational number \(\frac{97}{2 \times 5^{4}}\) will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Answer
Answer: d
29. The product of two consecutive natural numbers is always:
(a) prime number
(b) even number
(c) odd number
(d) even or odd
Answer
Answer: b
30. If the HCF of 408 and 1032 is expressible in the form 1032 x 2 + 408 × p, then the value of p is
(a) 5
(b) -5
(c) 4
(d) -4
Answer/ Explanation
Answer: b
Explaination:(b); [Hint. HCF of 408 and 1032 is 24, .-. 1032 x 2 + 408 x (-5)]
31. The number in the form of 4p + 3, where p is a whole number, will always be
(a) even
(b) odd
(c) even or odd
(d) multiple of 3
Answer
Answer: b
32. When a number is divided by 7, its remainder is always:
(a) greater than 7
(b) at least 7
(c) less than 7
(d) at most 7
Answer
Answer: c
33. (6 + 5 √3) – (4 – 3 √3) is
(a) a rational number
(b) an irrational number
(c) a natural number
(d) an integer
Answer
Answer: b
34. If HCF (16, y) = 8 and LCM (16, y) = 48, then the value of y is
(a) 24
(b) 16
(c) 8
(d) 48
Answer
Answer: a
35. According to the fundamental theorem of arith-metic, if T (a prime number) divides b2, b > 0, then
(a) T divides b
(b) b divides T
(c) T2 divides b2
(d) b2 divides T2
span style=”color: #ff00ff;”>Answer
Answer: a
36. The number ‘π’ is
(a) natural number
(b) rational number
(c) irrational number
(d) rational or irrational
Answer
Answer: c
37. If LCM (77, 99) = 693, then HCF (77, 99) is
(a) 11
(b) 7
(c) 9
(d) 22
Answer
Answer: a
38. Euclid’s division lemma states that for two positive integers a and b, there exist unique integer q and r such that a = bq + r, where r must satisfy
(a) a < r < b
(b) 0 < r ≤ b
(c) 1 < r < b
(d) 0 ≤ r < b
Answer
Answer: d
39. For positive integers a and 3, there exist unique integers q and r such that a = 3q + r, where r must satisfy:
(a) 0 < r < 3
(b) 1 < r < 3
(c) 0 < r < 3
(d) 0 < r < 3
Answer
Answer: a
40. Find the greatest number of 5 digits, that will give us remainder of 5 when divided by 8 and 9 respectively.
(a) 99921
(b) 99931
(c) 99941
(d) 99951
Answer/ Explanation
Answer: c
Explaination: The greatest number will be multiple of LCM (8, 9)
LCM of 8 and 9 = 72
On verification we find that 99941 when divided by 72 leaves remainder 5.
41. For some integersp and 5, there exist unique integers q and r such that p – 5q + r. Possible values of r are
(a) 0 or 1
(b) 0, 1 or 2
(c) 0, 1, 2 or 3
(d) 0, 1, 2, 3 or 4
Answer/ Explanation
Answer: d
Explaination: According to Euclids division lemma, p – 5q + r, where 0 < r < 5
⇒ r = 0,1,2, 3, 4
So, possible values of r are 0, 1,2, 3 or 4.
42. If two positive integers a and b are written as a = x’y1 and b = xyi, where x, y are prime numbers, then HCF(a, b) is
Also, find LCM of (a, b). [NCERT Exemplar Problems; Delhi 2019]
(a) xy
(b) xy²
(c) x3y3
(d) x²y²
Answer/ Explanation
Answer: b
Explaination: Here, a = x3y² and b = xy3
⇒ a=x × x × x × y × y
and b = xy × y × y
∴ HCF(a, b) = x × y × y
= x × y² = xy²
LCM = x3y3
43. If two positive integers p and q can be expressed as p = ab² and q = c3b; where a, b being prime numbers, then LCM (p, q) is equal to [NCERT Exemplar Problems]
(a) ab
(b) crb²
(c) a3b²
(d) c²b3
Answer/ Explanation
Answer: c
Explaination:LCM (p, q) = a3b²
44. The ratio between the LCM and HCF of 5, 15, 20 is:
(a) 9 : 1
(b) 4:3
(c) 11:1
(d) 12:1
Answer/ Explanation
Answer: d
Explaination:
5, 15 = 5 × 3, 20 = 2 × 2 × 5
LCM(5, 15, 20) = 5 × 3 × 2 × 2 = 60
HCF(5, 15, 20) = 5
![]()
45. Two alarm clocks ring their alarms at regular intervals of 50 seconds and 48 seconds. If they first beep together at 12 noon, at what time will they beep again for the first time ?
(a) 12.20 pm
(b) 12.12 pm
(c) 12.11pm
(d) none of these
Answer/ Explanation
Answer: d
Explaination:
LCM of 50 and 48 = 1200
∴ 1200 sec = 20 min
Hence at 12.20 pm they will beep again for the first time.
46. If A = 2n + 13, B = n + 7, where n is a
natural number, then HCF of A and B is:
(a) 2
(b) 1
(c) 3
(d) 4
Answer/ Explanation
Answer: b
Explaination:
Taking different values of n we find
that A and B are coprime.
∴ HCF = 1
47. There are 576 boys and 448 girls in a school that are to be divided into equal sections of either boys or girls alone. The total number of sections thus formed are:
(a) 22
(b) 16
(c) 36
(d) 21
Answer/ Explanation
Answer: b
Explaination:
HCF of 576 and 448 = 64
∴ Number of sections = \(=\frac{576}{64}+\frac{448}{64}\)
= 9 + 7 = 16
48. The HCF of 2472, 1284 and a third number N is 12. If their LCM is 23 x 32 x 5 x 103 x 107, then the number Nis :
(a) 22 x 32 x 7
(b) 22 x 33 x 103
(c) 22 x 32 x 5
(d) 24 x 32 x ll
Answer/ Explanation
Answer: c
Explaination:
2472 = 23 × 3 × 103
1284 = 2² × 3 × 107
∵ LCM = 23 × 3² × 5 × 103 × 107
∴ N = 2² × 3² × 5 = 180
49. Two natural numbers whose difference is 66 and the least common multiple is 360, are:
(a) 120 and 54
(b) 90 and 24
(c) 180 and 114
(d) 130 and 64
Answer/ Explanation
Answer: b
Explaination:
Difference of 90 and 24 = 66
and LCM of 90 and 24 = 360
∴ Numbers are 90 and 24.
50. HCF of 52 x 32 and 35 x 53 is:
(a) 53 x 35
(b) 5 x 33
(c) 53 x 32
(d) 52 x 32
Answer/ Explanation
Answer: d
Explaination:
HCF of 5² × 3² and 35 × 53
= 5² × 3²
51. A number 10x + y is multiplied by another number 10a + b and the result comes as 100p + 10q + r, where r = 2y, q = 2(x + y) and p = 2x; y < 5, q ≠ 0. The value of 10a + b may be _______.
Answer/ Explanation
Answer:
Explaination:
(10x + y)(10a + b) = 100p + 10q + r
⇒ (10x + y)(10a + b) = 100 × 2x + 10 × 2(x + y) + 2y
⇒ (10x + y)(lOa + b) = 200x + 20(x + y) + 2y
⇒ (10x + y)(10a + b) = 220x + 22y
⇒ (10x + y)(\0a + b) = 22(10x + y)
⇒ 10a + b = 22
52. If the HCF of 55 and 99 is expressible in the form 55m – 99, then the value of m is _______.
Answer/ Explanation
Answer:
Explaination:
55 = 5 × 11, 99 = 9 × 11
∴ HCF(55, 99) = 11
ATQ, 55m – 99 = 11
55 × 2-99 = 11
m = 2
53. Euclid’s division lemma states for any two positive integers a and b, there exists integers q and r such that a = bq + r. If a = 5, b = 8, then write the value of q and r.
Answer/ Explanation
Answer:
Explaination:
Using Euclid’s division lemma, we get
a = bq + r
5 = 8 × 0 + 5
q = 0 and r = 5
54. If a and b are two positive integers such that a = 14b. Find the HCF of a and b.
Answer/ Explanation
Answer:
Explaination:
We can write
a = 14b + 0
∵ remainder is 0
∴ HCF is b.
55. Find HCF of 1001 and 385.
Answer/ Explanation
Answer:
Explaination:
1001 =385 × 2 + 231
385 =231 × l + 154
231 =154 × 1 + 77
154 = 77 × 2 + 0
∴ HCF =77
56. 4 Bells toll together at 9.00 am. They toll after 7, 8, 11 and 12 seconds respectively. How many times will they toll together again in the next 3 hours?
(a) 3
(b) 4
(c) 5
(d) 6
Answer/ Explanation
Answer: c
Explaination:
LCM of 7, 8, 11, 12 = 1848
∴ Bells will toll together after every 1848 sec.
∴ In next 3 hrs, number of times the bells will toll together
\(=\frac{3 \times 3600}{1848}\) = 5.84
⇒ 5 times.
57. The HCF and LCM of two numbers are 33 and 264 respectively. When the first number is completely divided by 2 the quotient is 33. The other number is ________ .
Answer/ Explanation
Answer:
Explaination:First number = 2 × 33 = 66

58. Given that LCM (91, 26) = 182, then HCF (91, 26) is _______.
Answer/ Explanation
Answer:
Explaination:
LCM (91, 26) × HCF (91, 26) = 91 × 26
182 × HCF (91, 26) = 91 × 26
⇒ HCF (91, 26) = \(=\frac{91 \times 26}{182}\)
⇒ HCF (91, 26) = 13
59. Find the LCM of smallest prime and smallest odd composite natural number.
Answer/ Explanation
Answer:
Explaination:
Smallest prime number = 2
Smallest composite odd number = 9
LCM of 2 and 9 = 2 × 9 = 18
60. Decompose 32760 into prime factors.
Answer/ Explanation
Answer:
Explaination:
32760 =2 × 2 × 2 × 3 × 3 × 5 × 7 × 13
= 23 × 32 × 5 × 7 × 13
61. Write the sum of exponents of prime factors in the prime factorisation of 250.
Answer/ Explanation
Answer:
Explaination:
250 = 2 × 53
∴ Sum of exponents =1 + 3 = 4
62. Complete the missing entries in the following factor tree:
Answer/ Explanation
Answer:
Explaination:
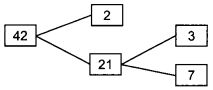
63. What is the HCF of smallest prime number and the smallest composite number? [CBSE 2018]
Answer/ Explanation
Answer:
Explaination:
The smallest prime number = 2
The smallest composite number = 4
∴ HCF of 2 and 4 = 2
64. If the prime factorisation of a natural number N is 24 × 34 × 53 × 7, write the number of consecutive zeroes in N.
Answer/ Explanation
Answer:
Explaination:
Number of consecutive zeroes = zeroes in 23 × 53 = zeroes in (10)3 = 3
65. If product of two numbers is 3691 and their LCM is 3691, find their HCF.
Answer/ Explanation
Answer:
Explaination:
![]()
66. If p and q are two coprime numbers, then find the HCF and LCM of p and q.
Answer/ Explanation
Answer:
Explaination:
∵ p and q are co-prime numbers
∴ Common factor of p and q = 1
⇒ HCF of p and q = 1
![]()
67. The HCF of 45 and 105 is 15. Write their LCM.
Answer/ Explanation
Answer: b
Explaination:
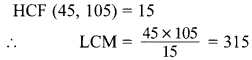
68. The HCF of two numbers is 145 and their LCM is 2175. If one number is 725, then find the other number.
Answer/ Explanation
Answer:
Explaination:
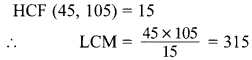
69. Can two numbers have 18 as their HCF and 380 as their LCM? Give reason. [NCERT Exemplar Problems]
Answer/ Explanation
Answer:
Explaination:
No, because HCF is always a factor of LCM. But 18 is not a factor of 380.
70. Find the largest number that divides 2053 and 967 and leaves a remainder of 5 and 7 respectively.
Answer/ Explanation
Answer:
Explaination:
Required number is HCF of 2053 – 5 and 967 – 7 = HCF of 2048 and 960 = 64
71. The decimal expansion of the rational number \(\frac{14587}{1250}\) will terminate after [NCERT Exemplar Problems]
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Answer/ Explanation
Answer:
Explaination:
72. Which of the following rational numbers have a terminating decimal expansion?
Answer/ Explanation
Answer:
Explaination:
![]()
The denominator 26 × 52 is 0f the form 2m × 5n where m and n are non-negative integers. Hence, it is a terminating decimal expansion.
73. The decimal expansion of number \(\frac{441}{2^{2} \times 5^{3} \times 7}\) has _______ decimal representation.
Answer/ Explanation
Answer:
Explaination:
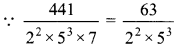
The denominator 26 × 52 is 0f the form 2m × 5n where m and n are non-negative integers.
74. From the following, the rational number whose decimal expansion terminating is:
Answer/ Explanation
Answer:
Explaination:
![]()
The denominator 25 × 51 is 0f the form 2m × 5n where m and n are non-negative integers. Hence, it is a terminating decimal expansion.
75. Without actually performing the long division, state whether the following rational numbers will have terminating decimal expansion or non-terminating repeating decimal expansion.
Answer/ Explanation
Answer:
Explaination:



76. Write whether \(\frac{2 \sqrt{45}+3 \sqrt{20}}{2 \sqrt{5}}\) on simplification gives an irrational or a rational number. [CBSE 2018 (C)]
Answer/ Explanation
Answer:
Explaination:

77. If \(\frac{p}{q}\) is a rational number (q ≠ 0), what is condition of q so that the decimal representation of \(\frac{p}{q}\) is terminating?
Answer/ Explanation
Answer:
Explaination:
For any rational number \(\frac{p}{q}\) with terminating decimal representation, the prime factorisation of q is of the form 2n.5m, where n and m are non-negative integers.
78. Find a rational number between √2 and √3 [Delhi 2019]
Answer/ Explanation
Answer:
Explaination:
Let p be rational number between √2 and √3
∴ √2 < p < √3
On squaring throughout, we have 2 < p² < 3
The perfect squares which lie between 2 and 3 are 2.25, 2.56, 2.89.
We have, 2 < 2.25 < 2.56 < 2.89 < 3
Taking square root throughout √2 < 1.5 < 1.6 < 1.7 < √3
The rational numbers between √2 and √3 are 1.5, 1.6 1.7 and more.