Refraction at Plane Surface Formulas
For those looking for Refraction at Plane Surface Formulas, this is the place. The Formulae List provided here on the topic Refraction at Plane Surface lays a stronger base of fundamentals. Learn the concept well and apply the formulae during your work and make your related calculations simple. Get to know about Brewster law, Laws of Refraction, Refraction by Slab, Total Internal Reflection, etc. You can answer any question framed on the concepts of Physics using our Physics Formulas.
Refraction at Plane Surface Formulae Sheet
If c → Velocity of light in air
V → Velocity of light in a medium
µ → Absolute refractive index of medium.
µm → Permeability of medium.
εm → Permittivity of a medium.
µ0 → Permeability of free space.
∈0 → Permittivity of free space.
c = \(\frac{1}{\sqrt{\varepsilon_{0} \mu_{0}}}\), v = \(\frac{1}{\sqrt{\varepsilon_{m} \mu_{m}}}\)
µ = \(\frac{c}{v}=\sqrt{\frac{\varepsilon_{m} \mu_{m}}{\varepsilon_{0} \mu_{0}}}=\sqrt{\varepsilon_{r} \mu_{r}}\)
refractive index of 2 w.r.t. 1
1µ2 = \(\frac{\mu_{2}}{\mu_{1}}=\frac{\mathrm{c} / \mathrm{v}_{2}}{\mathrm{c} / \mathrm{v}_{1}}=\frac{\mathrm{v}_{1}}{\mathrm{v}_{2}}\)
1. Laws of refraction
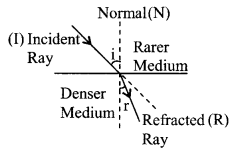
- Frequency (Colour) and phase not change (while wavelength and velocity changes) when light ray go from one medium to another medium.
- I, R & N are in a same plane.
- Snell’s law \(\frac{\sin i}{\sin r}={ }_{1} \mu_{2}=\frac{\mu_{2}}{\mu_{1}}=\frac{v_{1}}{v_{2}}=\frac{\lambda_{1}}{\lambda_{2}}\)
2. Total internal reflection
It occur when i > θc (Critical angle) At θc, the refracted ray just grazes the boundary between two media.
sin µ1θc = µ2 sin 90°
θc = sin-1\(\frac{\mu_{2}}{\mu_{1}}\)
If µ2 = 1 (air), θc = sin-1\(\left(\frac{1}{\mu}\right)\)
3. Brewester law
When partially reflected & refracted rays makes 90° angle then both get polarised.
and ip = tan-1µ
4. Refraction by slab
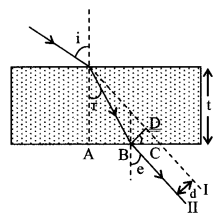
Lateral displacement d
d = t \(\frac{\sin (i-r)}{\cos r}\)
In fig. I & II lines are parallel.
5. Apparent depth (Dapp)
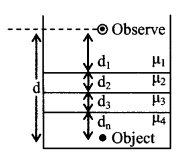
dapp = \(\frac{\mathrm{d}_{1}}{\mu_{1}}+\frac{\mathrm{d}_{2}}{\mu_{2}}+\frac{\mathrm{d}_{3}}{\mu_{3}} \ldots \ldots \frac{\mathrm{d}_{\mathrm{n}}}{\mu_{\mathrm{n}}}\)
Apparent shift (s)
s = d – dapp
6. Equivalent µ
µ = \(\frac{d_{\text {actual }}}{d_{\text {app. }}}=\frac{d_{1}+d_{2} \ldots \ldots . d_{n}}{\frac{d_{1}}{\mu_{1}}+\frac{d_{2}}{\mu_{2}} \ldots \ldots . \frac{d_{n}}{\mu_{n}}}=\frac{d}{\sum_{i=1}^{i=n} \frac{d_{i}}{\mu_{i}}}\)
Understand the refraction at the plane surface and many other related topics easily by accessing them from the sought after place of Formulas i.e. Onlinecalculator.guru