Solid And Liquid State Formulas
If you had full-fledged knowledge about the properties of solids and liquids topics? Then, you can master in solving the Solid And Liquid State questions very efficiently. Here, we have compiled the list of Solid And Liquid State Formulas to help you all make your calculations easily. So, go ahead and refer to the Solid And Liquid State Formulas Sheet & Tables.
Solve your chemistry problems fastly and efficiently taking the help of Chemistry Formulas and learn about the Concepts without much effort.
Solid And Liquid State Formulae Tables & Sheet
Students can learn more about the Solid State and Liquid State concepts by using the Solid And Liquid State Formulas. Must check the Solid And Liquid State Formulae Sheet and start using them while solving related problems. Indeed, the Solid And Liquid State Formulas List can help you revise the whole concept quickly and smartly.
1. Crystalline and amorphous solid:
- Internal arrangement of crystalline solid is regular, definite geometry, sharp m. p., cooling curve is discontinuous, show anisotropy.
- No regularity in the arrangement of particles in amorphous solid, no sharp m. p., cooling curve is continuous, show isotropy.
2. Classification of crystalline solids:
- Ionic [NaCl, KNO3],
- Metallic [Na, Al, Cu],
- Covalent [SiO2, diamond, quartz],
- Molecular [I2]
- Solid [CO2, S8].
3. Number of atoms per unit cell:
simple cubic = 1
fee = 4, bcc = 2, hep = 6
4. Crystal system
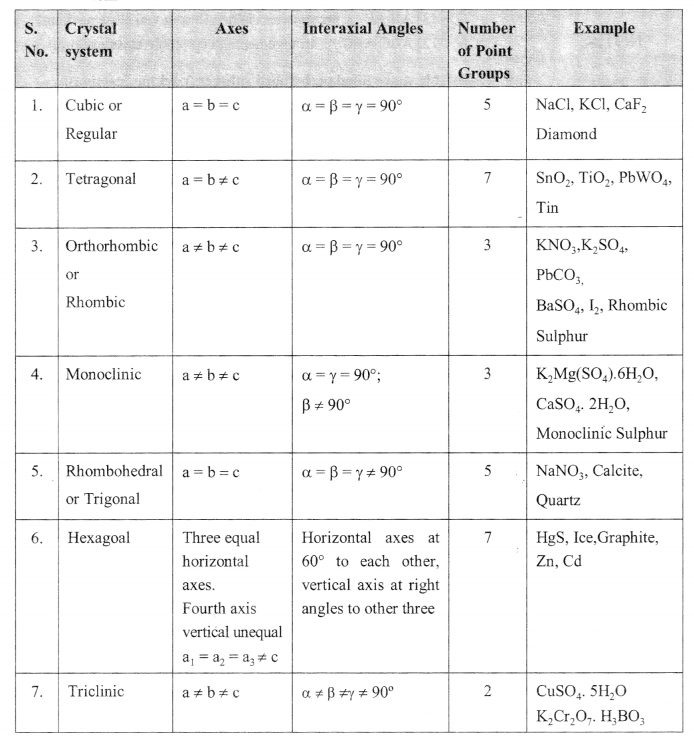
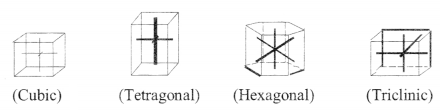
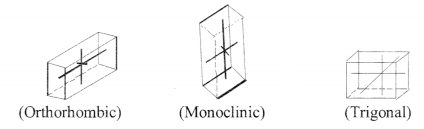
5. Close packing in three dimensions:
[CN = 12] AB AB …. arrangement in hep (hexagonal close packing)
[CN = 12] ABC ABC …. arrangement in ccp (cubic close packing)
6. Available space filled up by hard spheres (packing fraction):
Simple cubic = \(\frac{\pi}{6}\) = 0.52
bcc = \(\frac{\pi \sqrt{3}}{8}\) = 0.68
fcc = \(\frac{\pi \sqrt{2}}{6}\) = 0.74
hcp = \(\frac{\pi \sqrt{2}}{6}\) = 0.74
dimond = \(\frac{\pi \sqrt{3}}{6}\) = 0.34
7. Radius ratio and co-ordination number (CN):
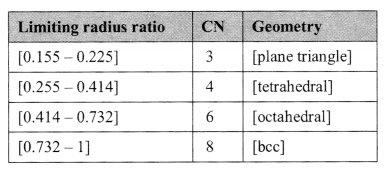
8. Atomic radius r and the edge of the unit cell:
Pure elements :
Simple cubic = r = \(\frac{a}{2}\)
bcc r = \(\frac{\sqrt{3} a}{4}\) fcc = \(\frac{\sqrt{2} a}{4}\)
9. Neighbour distance and edge of the unit cell:
simple cubic d = a; bcc d = \(\frac{\sqrt{3}}{2}\)a fcc d = \(\frac{\sqrt{2}}{2}\) a
10. Interstitial voids:
tetrahedral void:
\(\frac{r_{\text {void }}}{r_{\text {sphere }}}\) = 0.225
number of tetrahedral void = double the number of spheres octahedral void:
\(\frac{r_{\text {void }}}{r_{\text {sphere }}}\) = o.414
number of octahedral void = number of spheres
octahedral void < tetrahedral void
11. Density of the unit cell:
d = 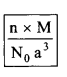
Where n = number of atoms in the unit cell,
M = atomic mass,
a = edge length,
N0 = Avogadro’s number
12. Bragg’s equation:
![]()
13. Elements of symmetry for cubic crystal:
centre of symmetry = 1
plane of symmetry = 9
axes of symmetry = 13
Total = 1 + 9 + 13 = 23
14. Crystal system:
Seven → cubic, orthorhombic, tetragonal, monoclinic, triclinic, hexagonal, rhombohedral
15. Weiss symbol of a given face:
e.g. \(\left(a: 2 b: \frac{1}{2} c\right)\) [where a, b, c, are unit intercepts of a unit face]
16. Miller indices:
e.g. Weiss symbol \(\left(a: 2 b: \frac{1}{2} c\right)\)
parameters \(\left[1,2, \frac{1}{2}\right]\), reciprocals \(\left[1, \frac{1}{2}, 2\right]\)
clear fraction [2, 1, 4] or [214]
17. Specific crystal structure:
NaCl (fcc), 6 : 6 co-ordination, 4 NaCl/unit cell
CsCl (cubic), 8 : 8 co-ordination, 1 CsCl/unit cell
Zns (fcc), 4 : 4 co-ordination, 4 ZnS/unit cell
[Zn2+ _ occupy 1/2 the tetrahedral voids]
CaF2, 8 : 4 co-ordination, 4 CaF2/unit cell
[F– occupy all the tetrahedral voids]
antifluorite Na2O (fee), 4 : 8 co-ordination 4 Na2O/unit cell
[Na+ occupy all the tetrahedral voids]
18. Shottky defect (stoichiometric):
Missing of ions from lattice points, density is decreased.
19. Frenkel defect (stoichiometric):
Ions are displaced to interstitial sites creating hole (No change in density)
20. F-centres:
Anions are missing and are occupied by electrons.
21. Magnetic properties:
diamagnetic:
All electrons are paired [repelled by magnetic field]
22. Paramagnetic:
Presence of unpaired electrons [attracted by magnetic field]
23. Ferromagnetic: Permanent magnetism [↑↑↑↑]
24. Antiferromagnetic: net magnetic moment is zero [↑↓↑↓ ]
25. Ferrimagnetic: net magnetic moment is there [↑↓↓↑↑]
26. Super conductivity:
They do not offer resistance to flow of current at very low temperature [2 – 5K]
Visit the Onlinecalculator.guru and get the go-to sheets of various concepts formulas for subjects like Chemistry Maths, Physics, etc. to learn more.