Viscosity Formulas
Viscosity is nothing but a fluid's resistance to flow. You need not bother about the topic of viscosity anymore as we have mentioned all the Viscosity Formulas completely. You can get a good grip on the concept after referring to the Viscosity Formulae Collection. If you are looking for help on related concepts of Physics access our Physics Formulas. Master the concept of Viscosity using the Cheat Sheets & Tables provided and try solving the problems at a faster pace.
Cheat Sheet & Tables for Viscosity
(i) The property of the liquid by virtue of which it opposes the relative motion between its adjacent layers is known as viscosity.
(ii) Internal tangential force which try to retard the relative motion between the layers is called viscous force.
F = ± η A \(\frac{\Delta \mathrm{v}_{\mathrm{x}}}{\Delta \mathrm{z}}\)
where η is constant called coefficient of viscosity of the liquid and \(\frac{\Delta \mathrm{v}_{\mathrm{x}}}{\Delta \mathrm{z}}\) is velocity gradient.
(iii) Viscosity comes into play only when there is a relative motion between the layers of the same material. This is why it does not act in solids.
1. Stokes law
(i) Stokes showed that if a small sphere of radius r is moving with a terminal velocity vT through a homogeneous medium (liquid or gas) of infinite extension, then the viscous force acting on the sphere is
F = 6πηrvT
where F is viscous force and vT is terminal velocity.
(ii) Viscous force acting upward = 6πηrvT. There is no acceleration so; the net force acting on it must be zero, i.e.,
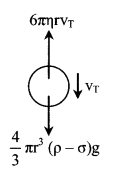
6πηrvT = \(\frac{4}{3}\) πr3(ρ – σ)g
or vT = \(\frac{2}{9} \frac{r^{2}(\rho-\sigma) g}{\eta}\)
vT ∝ r2
vT ∝ (ρ – σ)
vT ∝ \(\frac{1}{\eta}\)
Feel the extremely difficult topics too quite easy by accessing the concerned formulas from Onlinecalculator.guru and clear your doubts.