Work Energy Power Formulas
Work Energy Power are the most used terms in Physics. Feeling difficult while solving the Problems on the Work Energy Force? Don't Panic as you will get the Full List of Work Energy Power Formulas here. Understand the concepts better taking the help of the Work Energy Power Cheat Sheet & Tables provided. Formulae list prevailing covers topics like Work done by Spring Force, Variable Force, Constant Force, and others. Learn more concepts using our Physics Formulas and get a good hold of them.
Formula Sheet for Work Energy Power
1. Work done by constant force
W = Force × Component of displacement along force
= displacement × Component of force along displacement
W = FS cos θ ( θ is angle between \(\overrightarrow{\mathrm{F}} \text { and } \overrightarrow{\mathrm{S}}\))
W = \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{S}}\) S=r2-r(,
\(\overrightarrow{\mathrm{S}}=\overrightarrow{\mathrm{r}_{2}}-\overrightarrow{\mathrm{r}_{1}}\), displacement vector \(\Delta \overrightarrow{\mathrm{r}}\)
2. Work done by a variable force
W = \(\int_{r_{1}}^{r_{2}} \vec{F} \cdot d \vec{r}\) = Area under the F – r curve and position axis
W = \(\int_{x_{1}}^{x_{2}} F_{x} d x+\int_{y_{1}}^{y_{2}} F_{y} d y+\int_{z_{1}}^{z_{2}} F_{z} d z\)
3. Work done by spring force
W = –[\(\frac{1}{2}\)kx22 – \(\frac{1}{2}\)kx12] If x1 = 0 and x2 = x. Then W = \(\frac{1}{2}\) kx²
4. Energy
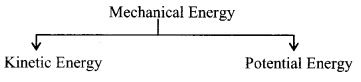
Kinetic Energy = \(\frac{1}{2}\)mv² = \(\frac{p^{2}}{2 m}\)
5. Work – energy theorem
The sum of the work done by all the forces acting on a particle is equal to the change in its K,E.
ΔW= (K. E.)f – (K. E.)i = ΔK = WC + WNC + WOther
6. Conservative force
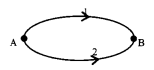
WAB, 1 = WAB, 2
means work done by conservative force does not depends on path, depends only on initial and final position.
Ex. Gravitational force, Electrostatics, etc.
7. Non conservative force
WAB, 1 ≠ WAB, 2
means work done by non conservative force depends on path.
Ex. Frictional force, viscous force, air resistance etc.
8. Potential energy
- Potential energy of a system is always defined corresponding to a conservative internal force.
- Change in P.E. = – Work done by the internal conservative force on the system. WC = – ΔU = – Wext
ΔU = Uf – Ui = – WC = –\(\int \overrightarrow{\mathrm{F}}_{\mathrm{c}} \cdot \overrightarrow{\mathrm{d}} \mathrm{r}\) - It is a respective quantity.
9. Gravitational P.E.
P.E. near the earth surface w.r.t. ground = mgh
spring potential energy = \(\frac{1}{2}\)kx²
⇒ Fc = – \(\vec{\nabla}\) U;
\(\vec{\nabla}=\frac{\partial}{\partial x} \hat{i}+\frac{\partial}{\partial y} \hat{j}+\frac{\partial}{\partial z} \hat{k}\)
10. Power
P = \(\frac{\mathrm{dW}}{\mathrm{dt}}=\overrightarrow{\mathrm{F}} \cdot \frac{\overrightarrow{\mathrm{d}} \mathrm{r}}{\mathrm{dt}}=\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{v}}\)
Want more Physics concepts formula sheets and tables for solving various problems? Then, visit this reliable site Onlinecalculator.guru and get all of them under one roof.