Binomial Expansion Calculator
Binomial Expansion Calculator is a free online tool that lets you solve the expansion of a binomial in the blink of an eye. Just enter the input term in the below box and tap on the calculate button to attain the result in Binomial Expansion.
Ex:
Here are some samples of Binomial Expansion calculations.
- Binomial Expansion of (1+2x)^10
- Binomial Expansion of (1+2x)^3
- Binomial Expansion of (1+2x^3)^5
- Binomial Expansion of (1+3x)^4
- Binomial Expansion of (1+4x)^6
- Binomial Expansion of (1+5i)^4
- Binomial Expansion of (1+h)^3
- Binomial Expansion of (1+x)^10
- Binomial Expansion of (1+x)^2
- Binomial Expansion of (1+x)^3
- Binomial Expansion of (1+x)^4
- Binomial Expansion of (1+x)^5
- Binomial Expansion of (1+x)^8
- Binomial Expansion of (10+7x)^2
- Binomial Expansion of (10-5b)^3
- Binomial Expansion of (10a+b)^6
- Binomial Expansion of (10x+y)^3
- Binomial Expansion of (10x-3y)^3
- Binomial Expansion of (10x-y)^2
- Binomial Expansion of (11-6x)^2
- Binomial Expansion of (11x+y)^3
- Binomial Expansion of (1-2x)^2
- Binomial Expansion of (1-2x)^5
- Binomial Expansion of (12x+y)^3
- Binomial Expansion of (12x-yz)^3
- Binomial Expansion of (1-2y)^2
- Binomial Expansion of (12y-5)^2
- Binomial Expansion of (13-2x)^2
- Binomial Expansion of (1-3x)^7
- Binomial Expansion of (15-4x)^3
- Binomial Expansion of (1-b^3)^3
- Binomial Expansion of (1-i)^10
- Binomial Expansion of (1-x)^3
- Binomial Expansion of (1-x)^4
- Binomial Expansion of (1-x)^5
- Binomial Expansion of (1-x)^6
- Binomial Expansion of (1-x^2)^2
- Binomial Expansion of (2+4i)^4
- Binomial Expansion of (2+5n^2)^2
- Binomial Expansion of (2+h)^2
Binomial Expansion Calculator: Feeling that the binomial expansion is difficult then you are wrong because expansion using the binomial theorem is quite easy. If not, make use of our Binomial Expansion Calculator and make your lengthy & complex expansion calculations faster & easier. Here, we have curated needy information on what is meant by binomial expansion and how to do it manually in detail.
What is Binomial Expansion in Algebra?
In Algebra, a polynomial with two terms is known as a binomial. The two terms are split up by either + or - symbol. By using the binomial theorem, we can define a binomial expansion of a given term. A binomial theorem is a mathematical theorem that gives the expansion of a binomial when it is raised to the positive integral power 'n'.
Thus, the formula for the expansion of a binomial defined by binomial theorem is given as:
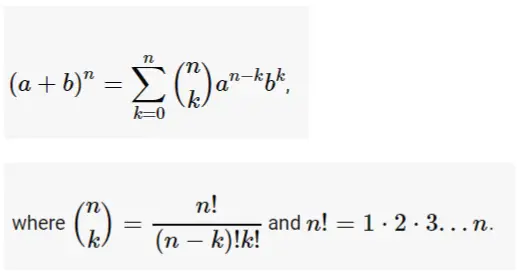
How to Expand Expression using the Binomial Theorem?
We can expand the expression (ex: (x+3)^4) using the binomial theorem, which is a formula that allows us to find the expanded form of a binomial raised to a positive integer 'n'.
The formula to expand the expression of a binomial is given above. Check the formula and simplify the given term into binomial expansion easily by hand.
If you want to get the result in just a few seconds then make use of our free online Binomial expansion calculator provided over here and also learn the concept entirely by using the detailed steps presented on the output page.
You can even find various maths free online calculators on our website onlinecalculator.guru by just clicking on this link. Make all your complex geometry & algebra calculations quite easy and quick by using our provided calculators.

FAQs on Binomial Expansion Calculator
1. What do you mean by binomial expansion?
The theorem that specifies the expansion of any power (a + b)^m of a binomial (a + b) as a certain sum of products a^ib^j, such as (a + b)^2 = a^2 + 2ab + b^2.
2. How to expand binomial expression using the binomial theorem easily?
You can expand expression easily by taking the help of the Binomial Expansion Calculator prevailing.
3. How do you do a binomial expansion on a calculator?
By just providing the input expression term in the input field and tapping on the calculate button in a Binomial Expansion Calculator helps you to get the result in just a fraction of seconds.