Arithmetic Sequence Calculator Geometric Sequence Calculator

Geometric Sequences Calculator

Use this handy tool Geometric Sequences Calculator to calculate the Sum of numbers that are in Geometric Progression. Simply provide the inputs in the respective input field and click on the enter button to avail output instantaneously.

Ex: 32,45,12,17,43,68,75,8,11,29

Geometric Sequences Calculator: If you are struggling to understand what Geometric Sequences are, don't worry as you will find everything related to it here. We included the concept of what a geometric progression is and how to find it manually. You can have detailed steps explaining how to do a summation of Geometric Sequence manually. Our Calculator is quite user friendly and all you need to do is just provide the sequence of numbers in Geometric Progression to avail their summation in no time.

What is a Geometric Sequence or Geometric Progression?

Geometric Sequence is also referred to as Geometric Progression. It is defined as the list of numbers in which each term in the sequence is multiplied by a constant non zero number called the common ratio "r".

Example: 1, 3, 9, 27, 81, …

The above sequence is an example of Geometric Progression in which each term in the sequence is multiplied by the common ratio 3 with the previous number.

How to find the Sum of a Geometric Sequence?

After learning about how to find a geometric sequence of a finite number you must be curious about how to find the sum of their geometric sequence. It may seem a bit difficult for you but following certain tricks will help you find the value in quite simple steps. For finite geometric progression i.e. For limited numbers the process of finding the sum can be quite simple.

Geometric Series or Sequence is generally denoted by the term an. The formula for Geometric Series would look like

S = ∑ a_n = a₁ + a₂ + a₃ + ... + a_m in which m is the total number of terms we want to sum.

Formula to find the sum of a geometric difference with the common ratio is expressed as

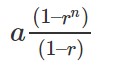
For more concepts and their relevant calculator tools to understand Math are provided at onlinecalculator.guru

FAQs on Geometric Sequences

1. What is meant by Geometric Sequence?

Geometric Sequence is defined as the list of numbers where each term in the sequence is multiplied by a constant non-zero number called the common ratio.

2. How to Calculate a Geometric Sequence?

You can calculate Geometric Sequence easily by taking the help of the formula i.e. a_n = a₁ * r^n-1

Where a_n is the nth term of the sequence

a₁ is the first term in the sequence

r is the common ratio

3. What is the formula to find the sum of a Geometric Sequence?

Formula to find the sum of a Geometric Sequence is given by

4. What does r mean in the Geometric Sequence?>

r is nothing but the common ratio in the Geometric Sequence.